题目列表(包括答案和解析)
（本小题满分12分）
如图，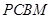
是直角梯形，
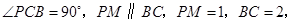又
，
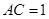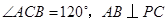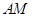，直线
与直线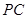
所成的角为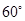
．
（Ⅰ）求证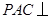：平面
平面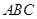
；
（Ⅱ）求二面角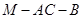
的大小；
（本小题满分12分）如图，在竖直平面内有一个“游戏滑道”，空白部分表示光滑滑道，黑色正方形表示障碍物，自上而下第一行有1个障碍物，第二行有2个障碍物，……，依次类推．一个半径适当的光滑均匀小球从入口A投入滑道，小球将自由下落，已知小球每次遇到正方形障碍物上顶点时，向左、右两边下落的概率都是
．记小球遇到第
行第
个障碍物（从左至右）上顶点的概率为
．
（Ⅰ）求
，
的值，并猜想的表达式（不必证明）；
（Ⅱ）已知
，设小球遇到第6行第个障碍物（从左至右）上顶点时，
得到的分数为
，试求
的分布列及数学期望．
（本小题满分12分）
如图， 
是直角三角形，
，
交
于点
，
平面
，
，
．
（1）证明：
；
（2）求平面
与平面所成的锐二面角的余弦值．
（本小题满分12分）
如图，是总体的一样本频率分布直方图，且在[15,18）内频数为8。
（1）求样本容量；
（2）若在[12,15）内小矩形面积为0.06，求在[12,15）内的频数；
（3）求样本[18,33]内的频率。
（本小题满分12分）
如图，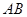
是底部
不可到达的一个塔型建筑物，
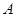为塔的最高点．现需在对岸测出塔高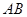，甲、乙两同学各提出了一种测量方法，甲同学的方法是：选与塔底在同一水平面内的一条基线
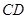，使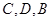
三点不在同一条直线上，测出
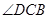及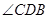
的大小（分别用
表示测得的数据）以及
间的距离（用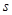
表示测得的数据），另外需在点
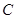测得塔顶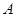的仰角（用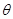
表示测量的数据），就可以求得塔高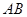．乙同学的方法是：选一条水平基线
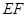，使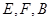
三点在同一条直线上．在
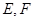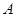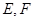处分别测得塔顶的仰角（分别用表示测得的数据）以及间的距离（用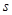表示测得的数据），就可以求得塔高．
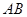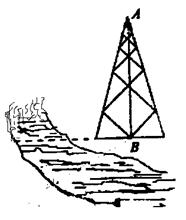
请从甲或乙的想法中选出一种测量方法，写出你的选择并按如下要求完成测量计算：①画出测量示意图；②用所叙述的相应字母表示测量数据，画图时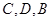按顺时针方向标注，
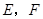按从左到右的方向标注；③求塔高．
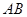一、
C A CBC A D AB D B A
二、
13．5;
14．
;
15． 36; 16．20
三、
17．解：（1）依题意得：
所以：
，……4分
|
，则
，
,
，…………8分
……………10分
，
，
………………………………………………………………12分
；……………………6分
……………………7分
………8分
＝
，…11分
；……………………12分
，所以
平面
，
，
平面
平面
平面
平面
，所以点
到平面
平面
的长为所求，………………………………………………………………………6分
为二面角
的平面角，
，
＝1，
，由
，得到
，
是二面角
的平面角，
，…………………………………………………………………11分
。……12分
的公差为
，依题意得：
，
，所以
，…………………3分
，
，
；…………………………………………………………………6分
，因为
，所以数列
是递增数列，…8分
时，
取得最小值，
，
，即
的取值范围是
。………………………………………12分
的坐标为
，则点
的坐标为
，点
的坐标为
，
，所以
，得到：
，注意到
不共线，所以轨迹方程为
；…………………………………5分
是轨迹C上的任意一点，则以
为直径的圆的圆心为
，
存在，设其方程为
，直线
截得的弦为
…………………………………………7分
为定值，则
，即
，
，……………………………………………………9分
时，存在直线
，截得的弦长为
，
时，不存在满足条件的直线
，
，……2分
，
或
时取得极大值，所以
，
的取值范围是：
；………………………………………………………4分
，
，
；……9分
都有
，
，
,
。………………………………………14分