
题目列表(包括答案和解析)
| AP |
| BP |
| PC |
4
| ||
| 5 |
| 2 |
| 2 |
| 1 |
| 2 |
在平面直角坐标系中,若![]() ,且
,且![]() ,
,
(1)求动点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(2)已知定点![]() ,若斜率为
,若斜率为![]() 的直线
的直线![]() 过点
过点![]() 并与轨迹
并与轨迹![]() 交于不同的两点
交于不同的两点![]() ,且对于轨迹
,且对于轨迹![]() 上任意一点
上任意一点![]() ,都存在
,都存在![]() ,使得
,使得![]() 成立,试求出满足条件的实数
成立,试求出满足条件的实数![]() 的值。
的值。
(本题满分14分)
已知点 是⊙
是⊙ :
: 上的任意一点,过
上的任意一点,过 作
作 垂直
垂直 轴于
轴于 ,动点
,动点 满足
满足 。
。
(1)求动点 的轨迹方程;
的轨迹方程;
(2)已知点 ,在动点
,在动点 的轨迹上是否存在两个不重合的两点
的轨迹上是否存在两个不重合的两点 、
、 ,使
,使 (O是坐标原点),若存在,求出直线
(O是坐标原点),若存在,求出直线 的方程,若不存在,请说明理由。
的方程,若不存在,请说明理由。
已知 、
、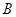 分别是直线
分别是直线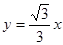 和
和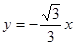 上的两个动点,线段
上的两个动点,线段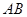 的长为
的长为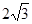 ,
,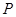 是
是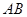 的中点.
的中点.
(1)求动点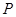 的轨迹
的轨迹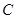 的方程;
的方程;
(2)过点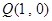 任意作直线
任意作直线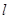 (与
(与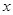 轴不垂直),设
轴不垂直),设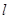 与(1)中轨迹
与(1)中轨迹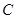 交于
交于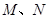 两点,与
两点,与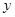 轴交于
轴交于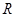 点.若
点.若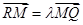 ,
,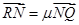 ,证明:
,证明: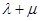 为定值.
为定值.
一、
C A CBC A D AB D B A
二、
13.5;
14. ;
15. 36; 16.20
;
15. 36; 16.20
三、
17.解:(1)依题意得:

所以: ,……4分
,……4分
|