
题目列表(包括答案和解析)
(本小题满分14分)
已知函数f(x)的定义域为 ,且同时满足:①f(1)=3;②
,且同时满足:①f(1)=3;② 对一切
对一切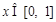 恒成立;③若
恒成立;③若 ,
,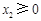 ,
,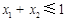 ,则
,则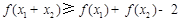 .
.
①求函数f(x)的最大值和最小值;
②试比较 与
与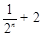
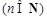 的大小;
的大小;
③某同学发现:当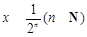 时,有
时,有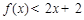 ,由此他提出猜想:对一切
,由此他提出猜想:对一切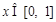 ,都有
,都有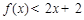 ,请你判断此猜想是否正确,并说明理由.
,请你判断此猜想是否正确,并说明理由.
(本小题满分14分)
已知函数f(x)=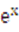 -kx,.
-kx,.
(1)若k=e,试确定函数f(x)的单调区间;
(2)若k>0,且对于任意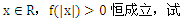 确定实数k的取值范围;[来源:学&科&网]
确定实数k的取值范围;[来源:学&科&网]
(3)设函数F(x)=f(x)+f(-x),求证:F(1)F(2)…F(n)>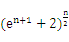 (
(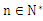 )。
)。
(本小题满分14分)
已知函数f(x)=-x3+3x2+9x+a.
(I)求f(x)的单调递减区间;
(II)若f(x)在区间[-2,2]上的最大值为20,求它在该区间上的最小值.
(本小题满分14分)
已知函数f(x)=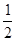 x
x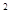 -ax + (a-1)
-ax + (a-1)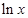 ,
,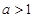 .
.
(I)讨论函数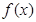 的单调性;
的单调性;
(II)若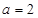 ,数列
,数列 满足
满足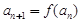 .
.
若首项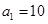 ,证明数列
,证明数列 为递增数列;
为递增数列;
若首项为正整数,数列 递增,求首项的最小值.
递增,求首项的最小值.
(本小题满分14分)已知函数f(x)=2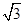 sinxcosx-2sin2x.
sinxcosx-2sin2x.
(1)求函数f(x)的最小正周期;
(2)求函数f(x)在区间[-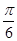 ,
,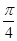 ]上的最大值和最小值.
]上的最大值和最小值.
一、
C A CBC A D AB D B A
二、
13.5;
14. ;
15. 36; 16.20
;
15. 36; 16.20
三、
17.解:(1)依题意得:

所以: ,……4分
,……4分
|