
题目列表(包括答案和解析)
(本小题满分12分)如图, 在直角梯形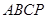 中,
中,
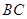 ∥
∥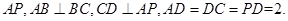
点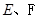 分别是
分别是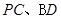 的中点,现将
的中点,现将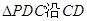 折起,使
折起,使 ,
,
(1)求证: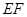 ∥平面
∥平面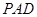 ;
;
(2)求点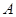 到平面
到平面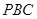 的距离.
的距离.
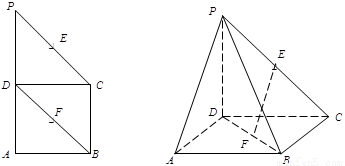
(理)(本小题8分)如图,在四棱锥 中,底面
中,底面 是矩形,
是矩形,
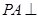 平面
平面 ,
,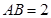 ,
, ,以
,以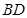 的中点
的中点 为球心、
为球心、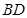 为直径的球面交
为直径的球面交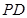 于点
于点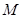 .
.
(1) 求证:平面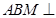 平面
平面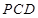 ;
;
(2)求点 到平面
到平面 的距离.
的距离.
证明:(1)由题意,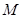 在以
在以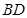 为直径的球面上,则
为直径的球面上,则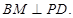
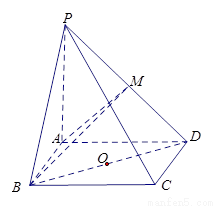
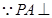 平面
平面 ,则
,则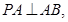
又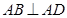 ,
,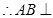 平面
平面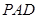 ,
,
∴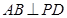 ,
,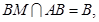
 平面
平面 ,
,
∴平面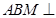 平面
平面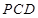 . (3分)
. (3分)
(2)∵ 是
是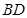 的中点,则
的中点,则 点到平面
点到平面 的距离等于点
的距离等于点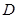 到平面
到平面 的距离的一半,由(1)知,
的距离的一半,由(1)知,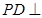 平面
平面 于
于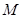 ,则线段
,则线段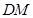 的长就是点
的长就是点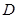 到平面
到平面 的距离
的距离

∵在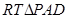 中,
中,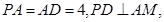
∴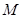 为
为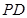 的中点,
的中点,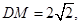 (7分)
(7分)
则点 到平面
到平面 的距离为
的距离为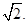 (8分)
(8分)
(其它方法可参照上述评分标准给分)
.(本小题满分12分)
如图5所示的多面体是由底面为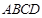 的长方体被截面
的长方体被截面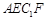 所截
所截
而得到的,其中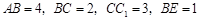 .
.
(1)求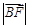 ;
;
(2)求点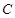 到平面
到平面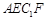 的距离.
的距离.
(本题满分12分)本题共有2个小题,第1小题满分8分,第2小题满分4分.
在正四棱柱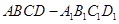 中,已知底面
中,已知底面 的边长为2,点P是
的边长为2,点P是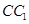 的中点,直线AP与平面
的中点,直线AP与平面 成
成 角.
角.
(文)(1)求 的长;
的长;
(2)求异面直线 和AP所成角的大小.(结果用
和AP所成角的大小.(结果用
反三角函数值表示);
(理)(1)求异面直线 和AP所成角的大小.(结果用
和AP所成角的大小.(结果用
反三角函数值表示) ;
(2)求点 到平面
到平面 的距离.
的距离.

(本小题满分12分)
在直三棱柱中,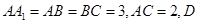 是
是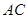 中点.
中点.
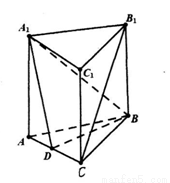
(1)求证: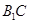 //平面
//平面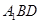 ;
;
(2)求点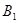 到平面
到平面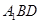 的距离;
的距离;
(3)求二面角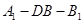 的余弦值.
的余弦值.
一、CABCB BDADD AC
二、13. 0.1;14. ;15. 36;16.存在,通项公式
;15. 36;16.存在,通项公式 。
。
三、
17.解:(1)依题意得:

得: ,
,
所以: ,即
,即 ,………………………………4分
,………………………………4分
|