题目列表(包括答案和解析)
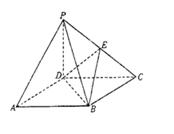
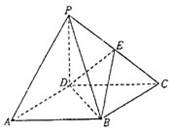
如图，四棱锥P—ABCD的底面ABCD是正方形，侧棱PD⊥底面ABCD，PD=DC，E是PC的中点.
（1）证明PA//平面BDE；
（2）求二面角B—DE—C的平面角的余弦值；
（3）在棱PB上是否存在点F，使PB⊥平面DEF？证明你的结论.
（08年龙岩一中冲刺理）（12分）
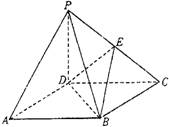
如图，四棱锥P―ABCD的底面ABCD是正方形，侧棱PD⊥底面ABCD，PD=DC，E是PC的中点．
（1）证明PA//平面BDE；
（2）求二面角B―DE―C的大小；
（3）在棱PB上是否存在点F，使PB⊥平面DEF？证明你的结论．
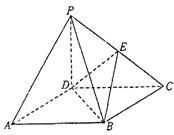如图，四棱锥P-ABCD的底面ABCD是正方形，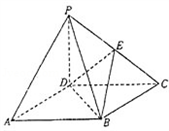
一、ABCBC AABBC
二、11.
12. 13 13. 
14.85,2
15.
16. 
17. (
，3)
三、18. 解：（1）
………………3分
最小正周期
………………5分
递减区间为
………………7分
（2）
………………10分
………………12分
得m的取值范围是
………………14分
19.
对应的事件为：男的摸到红球且女的一次摸到红球，
………………5分
0
10
20
50
60
P
=16.8
20. 解（1）以D为坐标原点，分别以DA、DC、DP所在直线为x轴、y轴、z轴建立空间直角坐标系，设PD=DC=2，则A（2，0，0），P（0，0，2），E（0，1，1），…………2分
B（2，2，0） 
设 
是平面BDE的一个法向量，
则由
………………4分
∵
…………5分
（2）由（Ⅰ）知
是平面BDE的一个法向量，又
是平面DEC的一个法向量.
………………7分
设二面角B―DE―C的平面角为
，由图可知
∴
故二面角B―DE―C的余弦值为
………………10分
（3）∵
∴
假设棱PB上存在点F，使PB⊥平面DEF，设
，
则
，
由
………………13分
∴
………………14分
即在棱PB上存在点F，
PB，使得PB⊥平面DEF ………………15分
用几何法证明酌情给分
21．
………………5分
|
时，
在
上是增函数 ………………6分
时，由已知成立；
时命题成立，即
成立，
时，由①得
，这就是说
时命题成立.
都成立 …………9分
得
……10分
时，
故
<0 得g(x)在
是减函数，
>0,即
>0