
题目列表(包括答案和解析)
将![]() 个正整数
个正整数![]() 填入
填入![]() 方格中,使其每行,每列,每条对角线上的数的和相等,这个正方形叫做
方格中,使其每行,每列,每条对角线上的数的和相等,这个正方形叫做![]() 阶幻方.记
阶幻方.记![]() 为
为![]() 阶幻方对角线的和,如右图就是一个
阶幻方对角线的和,如右图就是一个![]() 阶幻方,可知
阶幻方,可知![]() 则
则![]()
A.![]()
B.![]()
C.![]()
D.![]()
将连续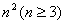 个正整数填入
个正整数填入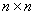 的方格中,使其每行、每列、每条对角线上的各数
的方格中,使其每行、每列、每条对角线上的各数
|
8 |
3 |
4 |
|
1 |
5 |
9 |
|
6 |
7 |
2 |
之和都相等,这个正方形叫做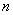 阶幻方数阵,记
阶幻方数阵,记 为
为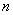 阶幻方数阵对角线上
阶幻方数阵对角线上
各数之和,如图就是一个3阶幻方数阵,可知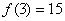 。若将等差数列3,4,5,6,
。若将等差数列3,4,5,6, 的前16 项填入
的前16 项填入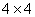 方格中,可得到一个4阶幻方数阵,则
方格中,可得到一个4阶幻方数阵,则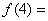 ( )
( )
A.44 B.42 C.40 D.36
将连续n2(n≥3)个正整数填入n×n的方格中,使其每行、每列、每条对角线上的各数之和都相等,这个正方形叫做n阶幻方数阵,记f(n)为n阶幻方数阵对角线上各数之和,如图就是一个3阶幻方数阵,可知f(3)=15.若将等差数列3,4,5,6,…,的前16项填入4×4方格中,可得到一个4阶幻方数阵,则f(4)=

44
42
40
36
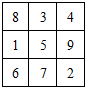 将连续n2(n≥3)个正整数填入n×n方格中,使其每行.每列.每条对角线上的数的和都相等,这个正方形叫做n阶幻方数阵.记f(n)为n阶幻方数阵对角线上数的和,如右图就是一个3阶幻方数阵,可知f(3)=15.若将等差数列:3,4,5,6,…的前16项填入4×4方格中,可得到一个4阶幻方数阵,则其对角线上的和f(4)等于( )
将连续n2(n≥3)个正整数填入n×n方格中,使其每行.每列.每条对角线上的数的和都相等,这个正方形叫做n阶幻方数阵.记f(n)为n阶幻方数阵对角线上数的和,如右图就是一个3阶幻方数阵,可知f(3)=15.若将等差数列:3,4,5,6,…的前16项填入4×4方格中,可得到一个4阶幻方数阵,则其对角线上的和f(4)等于( )| A、44 | B、42 | C、40 | D、36 |
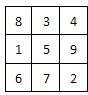 将连续n2(n≥3)个正整数填入n×n方格中,使其每行.每列.每条对角线上的数的和都相等,这个正方形叫做n阶幻方数阵.记f(n)为n阶幻方数阵对角线上数的和,如图就是一个3阶幻方数阵,可知f(3)=15.若将等差数列:3,4,5,6,…的前16项填入4×4方格中,可得到一个4阶幻方数阵,则其对角线上的和f(4)等于
将连续n2(n≥3)个正整数填入n×n方格中,使其每行.每列.每条对角线上的数的和都相等,这个正方形叫做n阶幻方数阵.记f(n)为n阶幻方数阵对角线上数的和,如图就是一个3阶幻方数阵,可知f(3)=15.若将等差数列:3,4,5,6,…的前16项填入4×4方格中,可得到一个4阶幻方数阵,则其对角线上的和f(4)等于一、选择题:
题号
1
2
3
4
5
6
7
8
9
10
答案










二、填空题:
11.  ; 12.
; 12.  ;
13.
;
13.  ;
;
14.  ;
15.
;
15.  ; 16. ③ ④ .
; 16. ③ ④ .
三、解答题:
17.解:(1)在 中,由
中,由 ,得
,得 , 又由正弦定理:
, 又由正弦定理: 得:
得: .
……………………4分
.
……………………4分
(2)由余弦定理: 得:
得: ,
,
即 ,解得
,解得 或
或 (舍去),所以
(舍去),所以 .
……8分
.
……8分
所以,


即 .
…………………12分
.
…………………12分
18.解:(1)依题意,双曲线 的方程可设为:
的方程可设为: 、
、 ,
,
则 解之得:
解之得: ,
,
所以双曲线 的方程为:
的方程为: .
……………………6分
.
……………………6分
(2)设 、
、 ,直线
,直线 与
与 轴交于
轴交于
 点,此点即为双曲线
点,此点即为双曲线 的右焦点,由
的右焦点,由 消去
消去 ,得
,得 ,
,
此方程的 且
且 ,
, ,
,
所以 、
、 两点分别在左、右支上,不妨设
两点分别在左、右支上,不妨设 在左支、
在左支、 在右支上 ………9分
在右支上 ………9分
则由第二定义知: ,
, , …………11分
, …………11分
所以


 ,即
,即 . ………14分
. ………14分
(亦可求出 、
、 的坐标,用两点间距离公式求.)
的坐标,用两点间距离公式求.)
19.(1)当点 为
为 的中点时,
的中点时, 与平面
与平面 平行.
平行.
∵在 中,
中, 、
、 分别为
分别为 、
、 的中点
的中点
∴ ∥
∥ 又
又 平面
平面 ,而
,而 平面
平面
∴ ∥平面
∥平面 .
……………………4分
.
……………………4分
(2)证明(略证):易证 平面
平面 ,又
,又 是
是 在平面
在平面 内的射影,
内的射影, ,∴
,∴ .
……………………8分
.
……………………8分
(3)∵ 与平面
与平面 所成的角是
所成的角是 ,∴
,∴ ,
, ,
, .
.
过 作
作 于
于 ,连
,连 ,则
,则 . …………………10分
. …………………10分
 易知:
易知: ,
, ,设
,设 ,则
,则 ,
, ,
,
在 中,
中, ,
,
得 .
………14分
.
………14分
解法二:(向量法)(1)同解法一
(2)建立图示空间直角坐标系,则 ,
,
 ,
, ,
, .
.
设 ,则
,则

 ∴
∴ (本小题4分)
(本小题4分)
(3)设平面 的法向量为
的法向量为 ,由
,由 ,
,
得: ,
,
依题意 ,∴
,∴ ,
,
得 .
(本小题6分)
.
(本小题6分)
20.解:(1) ,
,
∴可设 ,
,
因而 ①
①
由 得
得  ②
②
∵方程②有两个相等的根,
∴ ,即
,即 解得
解得  或
或
由于 ,
, (舍去),将
(舍去),将 代入 ① 得
代入 ① 得
 的解析式
的解析式 .
…………………6分
.
…………………6分
(2)
 =
= ,
,
∵ 在区间
在区间 内单调递减,
内单调递减,
∴ 在
在 上的函数值非正,
上的函数值非正,
由于 ,对称轴
,对称轴 ,故只需
,故只需 ,注意到
,注意到 ,∴
,∴ ,得
,得 或
或 (舍去)
(舍去)
故所求a的取值范围是 .
…………………11分
.
…………………11分
(3) 时,方程
时,方程 仅有一个实数根,即证方程
仅有一个实数根,即证方程 仅有一个实数根.令
仅有一个实数根.令
 ,由
,由 ,得
,得 ,
, ,易知
,易知 在
在 ,
, 上递增,在
上递增,在 上递减,
上递减, 的极大值
的极大值 ,
, 的极小值
的极小值 ,故函数
,故函数 的图像与
的图像与 轴仅有一个交点,∴
轴仅有一个交点,∴ 时,方程
时,方程 仅有一个实数根,得证.
……………………16分
仅有一个实数根,得证.
……………………16分
21.解:(1) , ……………………1分
, ……………………1分
 =
= .
……………………4分
.
……………………4分
(2) ,
……………………5分
,
……………………5分

 ,………7分
,………7分
∴数列 是
是 为首项,
为首项, 为公比的等比数列. ……………………8分
为公比的等比数列. ……………………8分
(3)由(2)知 , Sn =
, Sn = , ……………9分
, ……………9分
 =
= ∵0<
∵0< <1,∴
<1,∴ >0,
>0, ,0<
,0< <1,
<1, ,
,
∴
 ,
……………………11分
,
……………………11分
又当 时,
时, ,∴
,∴ , ……………………13分
, ……………………13分
∴
 <
< .……14分
.……14分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com