已知一隧道的截面是一个半椭圆面（如图所示），要保证车辆正常通行，车顶离隧道顶部至少要有0.5米的距离，现有一货车，车宽4米，车高2.5米。
（1）若此隧道为单向通行，经测量隧道的跨度是10米，则应如何设计隧道才能保证此货车正常通行？（2）圆可以看作是长轴短轴相等的特殊椭圆，类比圆面积公式，请你推测椭圆（a>b>0）的面积公式，并问，当隧道为双向通行（车道间的距离忽略不记）时，要使此货车安全通过，应如何设计隧道，才会使同等隧道长度下开凿的土方量最小？

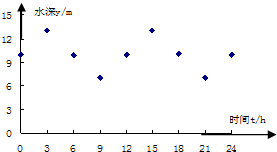某港口的水深y（m）是时间t （0≤t≤24，单位：h）的函数，下表是该港口某一天从0：00时至24：00时记录的时间t与水深y的关系：

t（h）	0：00	3：00	6：00	9：00	12：00	15：00	18：00	21：00	24：00
y（m）	10.0	13.0	9.9	7.0	10.0	13.0	10.1	7.0	10.0

经长时间的观察，水深y与t的关系可以用y=Asin（ωx+?）+h拟合．根据当天的数据，完成下面的问题：
（1）求出当天的拟合函数y=Asin（ωx+?）+h的表达式；
（2）如果某船的吃水深度（船底与水面的距离）为7m，船舶安全航行时船底与海底的距离不少于4.5m．那么该船在什么时间段能够进港？若该船欲当天安全离港，它在港内停留的时间最多不能超过多长时间．（忽略离港所需时间）
（3）若某船吃水深度为8m，安全间隙（船底与海底的距离）为2.5．该船在3：00开始卸货，吃水深度以每小时0.5m的速度减少，那么该船在什么时间必须停止卸货，驶向较安全的水域？

（2013•怀化二模）受日月引力的作用，海水会发生涨落，这种现象叫潮汐．在通常情况下，船在海水涨潮时驶进航道，靠近码头，卸货后返回海洋．某港口水的深度y（m）是时间t（0≤t≤24，单位：h）的函数，记作：y=f（t），下表是该港口在某季每天水深的数据：

t（h）	0	3	6	9	12	15	18	21	24
y（m）	10.0	13.1	9.9	7.0	10.1	13.0	10.0	7.0	10.0

经过长期观察y=f（x）的曲线可以近似地看做函数y=Asinωt+k的图象．
（Ⅰ）根据以上数据，求出函数y=f（t）的近似表达式；
（Ⅱ）一般情况下，船舶航行时船底离海底的距离为5m或5m以上时认为是安全的（船舶停靠时，船底只需不碰到海底即可），某船吃水深度（船底离水面的距离）为6.5m，如果该船想在同一天内安全进出港，问它至多能在港内停留多长时间（忽略进出港所需时间）？