如图甲所示，MN、PQ为间距L=0 .5m足够长的平行导轨，NQ⊥MN，导轨的电阻均不计。导轨平面与水平面间的夹角，NQ间连接有一个R=4Ω的电阻。有一匀强磁场垂直于导轨平面且方向向上，磁感应强度为B₀=1T。将一根质量为m=0.05kg的金属棒ab紧靠NQ放置在导轨上，且与导轨接触良好。现由静止释放金属棒，当金属棒滑行至cd处时达到稳定速度，已知在此过程中通过金属棒截面的电量q=0.2C，且金属棒的加速度a与速度v的关系如图乙所示，设金属棒沿导轨向下运动过程中始终与NQ平行。取g=10m/s²。求：

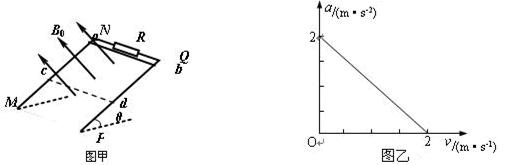
（1）金属棒与导轨间的动摩擦因数μ；

（2）cd离NQ的距离s；

（3）金属棒滑行至cd处的过程中，电阻R上产生的热量；

（4）若将金属棒滑行至cd处的时刻记作t=0，从此时刻起，让磁感应强度逐渐减小，为使金属棒中不产生感应电流，则磁感应强度B应怎样随时间t变化（写出B与t的关系式）。

如图甲所示，MN、PQ为间距L=0.5m足够长的平行导轨，NQ⊥MN，导轨的电阻均不计。导轨平面与水平面间的夹角θ=37°，NQ间连接有一个R=4Ω的电阻。有一匀强磁场垂直于导轨平面且方向向上，磁感应强度为B0=1T。将一根质量为m=0.05kg的金属棒ab紧靠NQ放置在导轨上，且与导轨接触良好。现由静止释放金属棒，当金属棒滑行至cd处时达到稳定速度，已知在此过程中通过金属棒截面的电量q=0.2C，且金属棒的加速度a与速度v的关系如图乙所示，设金属棒沿导轨向下运动过程中始终与NQ平行。（取g=10m/s2，sin37°=0.6，cos37°=0.8）。求：

（1）金属棒与导轨间的动摩擦因数μ（2）cd离NQ的距离s

（3）金属棒滑行至cd处的过程中，电阻R上产生的热量

（4）若将金属棒滑行至cd处的时刻记作t=0，从此时刻起，让磁感应强度逐渐减小，为使金属棒中不产生感应电流，则磁感应强度B应怎样随时间t变化（写出B与t的关系式）。

（20分）如图甲所示，MN、PQ为间距L=0.5m足够长的平行导轨，NQ⊥MN，导轨的电阻均不计，导轨平面与水平面间的夹角θ=37°，NQ间连接有一个R=4Ω的电阻。有一匀强磁场垂直于导轨平面且方向向上，磁感应强度为B₀=1T。将一根质量为m=0.05kg的金属棒ab紧靠NQ放置在导轨上，且与导轨接触良好。现由静止释放金属棒，当金属棒滑行至cd处时达到稳定速度，已知在此过程中通过金属棒截面的电量q=0.2C，且金属棒的加速度a与速度v的关系如图乙所示，设金属棒沿导轨向下运动过程中始终与NQ平行。（取g=10m/s²，sin37°=0.6，cos37°=0.8）。

求：

（1）金属棒与导轨间的动摩擦因数μ

（2）cd离NQ的距离s

（3）金属棒滑行至cd处的过程中，电阻R上产生的热量

（4）若将金属棒滑行至cd处的时刻记作t=0，从此时刻起，让磁感应强度逐渐减小，为使金属棒中不产生感应电流，则磁感应强度B应怎样随时间t变化

如图甲所示，MN、PQ为间距L="0" .5m足够长的平行导轨，NQ⊥MN，导轨的电阻均不计。导轨平面与水平面间的夹角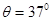，NQ间连接有一个R=4Ω的电阻。有一匀强磁场垂直于导轨平面且方向向上，磁感应强度为B₀=1T。将一根质量为m=0.05kg的金属棒ab紧靠NQ放置在导轨上，且与导轨接触良好。现由静止释放金属棒，当金属棒滑行至cd处时达到稳定速度，已知在此过程中通过金属棒截面的电量q=0.2C，且金属棒的加速度a与速度v的关系如图乙所示，设金属棒沿导轨向下运动过程中始终与NQ平行。取g=10m/s²。求：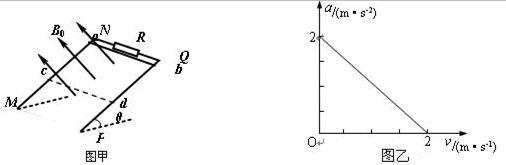

（1）金属棒与导轨间的动摩擦因数μ；
（2）cd离NQ的距离s；
（3）金属棒滑行至cd处的过程中，电阻R上产生的热量；
（4）若将金属棒滑行至cd处的时刻记作t=0，从此时刻起，让磁感应强度逐渐减小，为使金属棒中不产生感应电流，则磁感应强度B应怎样随时间t变化（写出B与t的关系式）。