
题目列表(包括答案和解析)
已知 的三个内角
的三个内角 所对的边分别为
所对的边分别为 ,且满足
,且满足 .
.
(1)求角 的大小;
的大小;
(2)若 ,
, 的面积为
的面积为 ,求
,求 的值.
的值.
【解析】本试题主要是考查了解三角形中正弦定理和正弦面积公式的求解运用。
(1)因为 ,利用正弦定理得到C的值。
,利用正弦定理得到C的值。
(2)根据 ,然后结合余弦定理得到C的值。
,然后结合余弦定理得到C的值。
已知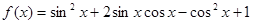
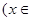 R
R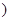 .
.
(1)求函数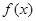 的最大值,并指出此时
的最大值,并指出此时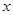 的值.
的值.
(2)若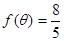 ,求
,求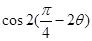 的值.
的值.
【解析】本试题主要考查了三角函数的性质的运用。(1)中,三角函数先化简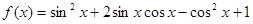 =
=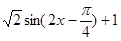 ,然后利用
,然后利用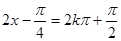 是,函数取得最大值
是,函数取得最大值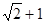 (2)中,结合(1)中的结论,然后由
(2)中,结合(1)中的结论,然后由
得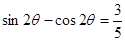 ,两边平方得
,两边平方得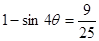 即
即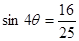 ,因此
,因此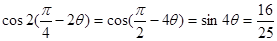
在 中,
中, 是三角形的三内角,
是三角形的三内角, 是三内角对应的三边,已知
是三内角对应的三边,已知 成等差数列,
成等差数列, 成等比数列
成等比数列
(Ⅰ)求角 的大小;
的大小;
(Ⅱ)若 ,求
,求 的值.
的值.
【解析】第一问中利用依题意 且
且 ,故
,故
第二问中,由题意 又由余弦定理知
又由余弦定理知

,得到 ,所以
,所以 ,从而得到结论。
,从而得到结论。
(1)依题意 且
且 ,故
,故 ……………………6分
……………………6分
(2)由题意 又由余弦定理知
又由余弦定理知
 …………………………9分
…………………………9分
即 故
故

 代入
代入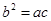 得
得

已知点A、B、C的坐标分别为A(3,0)、B(0,3)、C(cosα,sinα),
α∈( ,
, ).
).
(1)若| |=|
|=| |,求角α的值;
|,求角α的值;
(2)若 ·
· =-1,求
=-1,求 的值.
的值.
【解析】第一问中利用向量的模相等,可以得到角α的值。
第二问中, ·
· =-1,则化简
=-1,则化简 可知结论为
可知结论为
解:因为点A、B、C的坐标分别为A(3,0)、B(0,3)、C(cosα,sinα),
α∈( ,
, ).|
).| |=|
|=| |
所以α=
|
所以α= .
.
(2)因为 ·
· =-1,
=-1, 即
即 .
.
已知函数 ,
,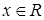 .
.
(Ⅰ)求 的最大值;
的最大值;
(Ⅱ)若 ,求
,求 的值.
的值.
【解析】第一问中利用化为单一三角函数可知,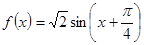 ,然后可得
,然后可得 第二问中,
第二问中,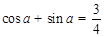 两边平方可知
两边平方可知 得到结论。
得到结论。 ……1分
……1分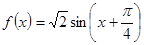 ……………1分
……………1分
 ,
, ………………1分
………………1分
(Ⅱ)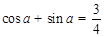


湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com