
题目列表(包括答案和解析)
(本小题满分10分)
已知三棱锥P-ABC中,PA⊥平面ABC,AB⊥AC,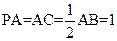 ,N为AB上一点,AB="4AN," M、S分别为PB,BC的中点.以A为原点,射线AB,AC,AP分别为x,y,z轴正向建立如图空间直角坐标系.
,N为AB上一点,AB="4AN," M、S分别为PB,BC的中点.以A为原点,射线AB,AC,AP分别为x,y,z轴正向建立如图空间直角坐标系.
(Ⅰ)证明:CM⊥SN;
(Ⅱ)求SN与平面CMN所成角的大小.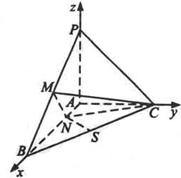
 ,N为AB上一点,AB="4AN," M、S分别为PB,BC的中点.以A为原点,射线AB,AC,AP分别为x,y,z轴正向建立如图空间直角坐标系.
,N为AB上一点,AB="4AN," M、S分别为PB,BC的中点.以A为原点,射线AB,AC,AP分别为x,y,z轴正向建立如图空间直角坐标系.
(选修4-4:坐标系与参数方程) (本小题满分10分)
在直角坐标系xoy中,直线![]() 的参数方程为
的参数方程为 (t为参数),在极坐标系(与直角坐标系xoy取相同的长度单位,且以原点O为极点,以x轴正半轴为极轴)中,圆C的方程为
(t为参数),在极坐标系(与直角坐标系xoy取相同的长度单位,且以原点O为极点,以x轴正半轴为极轴)中,圆C的方程为![]() .
.
(Ⅰ)求圆C的直角坐标方程;
(Ⅱ)设圆C与直线![]() 交于点A、B,若点P的坐标为
交于点A、B,若点P的坐标为![]() ,求|PA|+|PB|.
,求|PA|+|PB|.
23(本小题满分10分)
 已知三棱锥P-ABC中,PA⊥平面ABC,AB⊥AC,
已知三棱锥P-ABC中,PA⊥平面ABC,AB⊥AC,![]() ,N为AB上一点,AB=4AN, M、S分别为PB,BC的中点.以A为原点,射线AB,AC,AP分别为x,y,z轴正向建立如图空间直角坐标系.
,N为AB上一点,AB=4AN, M、S分别为PB,BC的中点.以A为原点,射线AB,AC,AP分别为x,y,z轴正向建立如图空间直角坐标系.
(Ⅰ)证明:CM⊥SN;
(Ⅱ)求SN与平面CMN所成角的大小.
24.(本小题满分10分)
将一枚硬币连续抛掷![]() 次,每次抛掷互不影响. 记正面向上的次数为奇数的概率为
次,每次抛掷互不影响. 记正面向上的次数为奇数的概率为![]() ,正面向上的次数为偶数的概率为
,正面向上的次数为偶数的概率为![]() .
.
(Ⅰ)若该硬币均匀,试求![]() 与
与![]() ;
;
(Ⅱ)若该硬币有暇疵,且每次正面向上的概率为![]() ,试比较
,试比较![]() 与
与![]() 的大小.
的大小.
(选修4-4:坐标系与参数方程) (本小题满分10分)
在直角坐标系xoy中,直线![]() 的参数方程为
的参数方程为 (t为参数),在极坐标系(与直角坐标系xoy取相同的长度单位,且以原点O为极点,以x轴正半轴为极轴)中,圆C的方程为
(t为参数),在极坐标系(与直角坐标系xoy取相同的长度单位,且以原点O为极点,以x轴正半轴为极轴)中,圆C的方程为![]() .
.
(Ⅰ)求圆C的直角坐标方程;
(Ⅱ)设圆C与直线![]() 交于点A、B,若点P的坐标为
交于点A、B,若点P的坐标为![]() ,求|PA|+|PB|.
,求|PA|+|PB|.
23(本小题满分10分)
 已知三棱锥P-ABC中,PA⊥平面ABC,AB⊥AC,
已知三棱锥P-ABC中,PA⊥平面ABC,AB⊥AC,![]() ,N为AB上一点,AB=4AN, M、S分别为PB,BC的中点.以A为原点,射线AB,AC,AP分别为x,y,z轴正向建立如图空间直角坐标系.
,N为AB上一点,AB=4AN, M、S分别为PB,BC的中点.以A为原点,射线AB,AC,AP分别为x,y,z轴正向建立如图空间直角坐标系.
(Ⅰ)证明:CM⊥SN;
(Ⅱ)求SN与平面CMN所成角的大小.
24.(本小题满分10分)
将一枚硬币连续抛掷![]() 次,每次抛掷互不影响. 记正面向上的次数为奇数的概率为
次,每次抛掷互不影响. 记正面向上的次数为奇数的概率为![]() ,正面向上的次数为偶数的概率为
,正面向上的次数为偶数的概率为![]() .
.
(Ⅰ)若该硬币均匀,试求![]() 与
与![]() ;
;
(Ⅱ)若该硬币有暇疵,且每次正面向上的概率为![]() ,试比较
,试比较![]() 与
与![]() 的大小.
的大小.
YC一、选择题:CDBBA, CBDDB, DB
二、填空题:13. ; 14.3 15.76 16.(1,e);e
; 14.3 15.76 16.(1,e);e
三、解答题:
17.解:(1)f‘(x)=-3x2+6x+9 …………2分
令 f‘(x)<0,解得x<-1或x>3。 …………4分
 函数f(x)的单调递减区间为(-
函数f(x)的单调递减区间为(- 。 …………5分
。 …………5分
(2) f(-2)=2+a , f(2)=22+a
f(-2)=2+a , f(2)=22+a
 f(2)>f(―2)
f(2)>f(―2)
 在(―1,3)上f‘(x)>
在(―1,3)上f‘(x)> f(x)在[―1,2]上单调递增。
f(x)在[―1,2]上单调递增。
又f(x)在[―2,1]上单调递减。 …………8分
∴f2)和f(-1)分别是f(x)在[―2,2]上的最大值和最小值。
于是有 22+a=20 , 解得a=-2
故f(x)=―x3+3x2+9x-2 …………10分
∴f(-1)=-7
即f(x)在[―2,2]上的最小值为-7 。 …………12分
18. 用 表示一天之内第
表示一天之内第 个部件需要调整的事件,
个部件需要调整的事件, ,则
,则 ,
, ……………………1分
……………………1分
以 表示一天之内需要调整的部件数,则
表示一天之内需要调整的部件数,则
(Ⅰ) ……4分
……4分
(Ⅱ) ………7分
………7分
(Ⅲ) ……………………8分
……………………8分
 …………9分
…………9分
 ……………………10分
……………………10分
 的分布列为
的分布列为

0
1
2
3
p
0.504
0.398
0.092
0.006
 …………12分
…………12分
19.(本小题满分12分)
解: (I)法一:取CC1的中点F, 连接AF, BF, 则AF∥C1D.
∠BAF为异面直线AB与C1D所成的角或其补角.……(1分)
∵△ABC为等腰直角三角形,
AC=2, ∴AB=2 .又∵CC1=2, ∴AF=BF=
.又∵CC1=2, ∴AF=BF= .
.
∵ ∴
∴
∴即异面直线AB与C1D所成的角为 (4分)
(4分)
法二:以C为坐标原点,CB,CA,CC1分别为x轴,y轴,z轴建立空间直角坐标系,则A(0,2,0),B(2,0,0),C1(0,0,2),D(0,2,1),∴ =(2,-2,0),
=(2,-2,0), =(0,2,-1).
=(0,2,-1).
由于异面直线AB与C1D所成的角为向量 与
与 的夹角或其补角.……(1分)
的夹角或其补角.……(1分)
设 与
与 的夹角为θ,
的夹角为θ,
|