题目列表(包括答案和解析)
C．选修4-4：坐标系与参数方程
在极坐标系下，已知圆O：
和直线
，
（1）求圆O和直线
的直角坐标方程；（2）当
时，求直线与圆O公共点的一个极坐标.
D．选修4-5：不等式证明选讲
对于任意实数
和
，不等式
恒成立，试求实数
的取值范围．
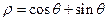和直线
，
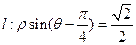的直角坐标方程；（2）当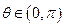
时，求直线与圆O公共点的一个极坐标.
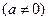和
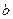，不等式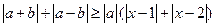
恒成立，试求实数
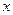的取值范围．C
[解析] 由基本不等式，得ab≤
＝
＝
－ab，所以ab≤
，故B错；
＋
＝
＝
≥4，故A错；由基本不等式得
≤
＝
，即
＋
≤
，故C正确；a2＋b2＝(a＋b)2－2ab＝1－2ab≥1－2×＝，故D错．故选C.
．定义域为R的函数
满足
，且当
时，
，则当
时，
的最小值为（ ）
（A）
（B）
（C）
（D）
．过点
作圆
的弦，其中弦长为整数的共有 （ ）
A.16条 B. 17条 C. 32条 D. 34条
DCABC CBBAC
11
12 23
13 2
14 4π
15
16解 （1）
1分
2分
由已知有
4分
6分
（2）
10分
= 
11分
= 
12分
17解：（1）设红球有
个，白球
个，依题意得 1分
，
3分
解得
故红球有6个．
5分
（2）记“甲取出的球的编号大”为事件A，
所有的基本事件有：(1，2)，(l，3)，(1，4)，
(2，1)，(2，3)，(2，4)，
(3，1)，(3，2)，(3，4)，
(4，1)，(4，2)，(4，3)，
共12个基本事件 8分
事件A包含的基本事件有：(1，2)，(1，3)，（1，4）（2，1），
（2，3），（3，1），（3，2）（4，1），
共8个基本事件
11分
所以，． 
12分
18解：（1）底面三边长AC=3，BC=4，AB=5，
∠ACB=90°，∴ AC⊥BC， （2分）
又在直三棱柱ABC－A1B1C1中，CC1⊥底面ABC，AC
底面ABC，∴CC1⊥AC，（3分）
BC．CC1平面BCC1，且BC 与CC1相交
∴ AC⊥平面BCC1； （5分）
而BC1平面BCC1
∴ AC⊥BC1 （6分）
（2）设CB1与C1B的交点为E，连结DE，∵ D是AB的中点，E是BC1的中点，
∴ DE//AC1， （8分）
∵ DE平面CDB1，AC1
平面CDB1，
∴ AC1//平面CDB1；（10分）
（3）
（11分）
=
-
（13分）
=20 （14分）
19解：（1）设椭圆的半长轴长．半短轴长．半焦距分别为a,b,c,则有
,
由椭圆定义，有
………1分
＝
……………………………2分
＝
……………………3分
≥
…………………………………………5分
＝
＝
……………………………………………6分
∴的最小值为。
（当且仅当
时，即
取椭圆上下顶点时，取得最小值 ）………………………………………7分
（2）设
的斜率为
，
则
，
…………………………………………8分
…………………………………………9分
∴
＝
及
…………………………………………10分
则＝
＝ 又
…………………………………………12分
∴
…………………………………………13分
故斜率的取值范围为（
） …………………………………………14分
20解：（1）
，……………………1分
即
，
即
，
，
…………………………………………2分
∴
为等差数列，
…………………………………………3分
又
，
…………………………………………4分
∴
，
…………………………………………5分
∴
…………………………………………7分
（2）
…………………………………………8分
当
时，
…………………………………………11分
，
…………………………………………13分
的整数部分为18。
…………………………………………14分
21解：（1）
………（1分）
由
解得：
………（2分）
当
或
时，
………（3分）
当
时，
………（4分）
所以，有两个极值点：
是极大值点，
；
………（5分）
是极小值点，
。 ………（6分）
(2) 过点
做直线
，与
的图象的另一个交点为A
，则
,即
………（8分）
已知有解
，则
解得
………（10分）
当
时，
；
………（11分）
当
时，
，
，
其中当
时，
；………（12分）
当
时，
……（13分）
所以，对任意的
，
的最小值为
（其中当时，）．……（14分）
（以上答案和评分标准仅供参考，其它答案，请参照给分）lf
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com