题目列表(包括答案和解析)
（本题12分）已知数列{an}中，a1=0，a2 =4，且an+2-3an+1+2an= 2n+1（
），
数列{bn}满足bn=an+1-2an．
（Ⅰ）求证:数列{
-
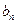}是等比数列；
（Ⅱ）求数列{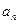
}的通项公式；
（Ⅲ）求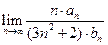
．
（本题12分）已知数列{an}中，a1=0，a2
=4，且an+2-3an+1+2an= 2n+1（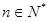
），
数列{bn}满足bn=an+1-2an．
（Ⅰ）求证:数列{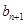
-
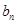}是等比数列；
（Ⅱ）求数列{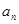
}的通项公式；
（Ⅲ）求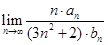
．
），
-
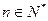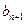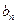}是等比数列；
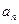}的通项公式；
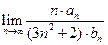．（本题满分12分） 已知数列{an}的前项和为Sn，且满足a1=1,2Sn=nan+1（1）求an； （2）设bn= ，求b1+b2+…+bn
（本题满分12分）
已知各项均为正数的数列{an}满足2a2n+1+3an+1an-2a2n=0（n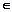
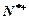）且a3+
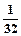是a2，a4的等差中项，数列{bn}的前n项和Sn=n2
（1）求数列{an}与{bn}的通项公式；
（2）若Tn=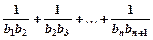
，求证：Tn<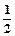
(3)若cn=-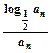
,T/n=c1+c2+…+cn,求使T/n+n
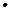2n+1>125成立的正整数n的最小值
一、选择题（每小题5分，共60 ）
DCAAD BCBAB CB
二、填空题（每小题4分，共16分）
13.100 14.0 15. 
16.B
三、解答题
17.
解
：
（3分）
又
（6分）
(2)
又
18．解：（Ⅰ）掷出点数x可能是：1，2，3，4.
则
分别得：
。于是
的所有取值分别为：0，1，4 .
因此
的所有取值为：0，1，2，4，5，8. …………………………………………2分
当
且
时，
可取得最大值8，
此时，
；
………………………………………………………4分
当
时且
时，可取得最小值 0.
此时
…………………………………………………………6分
（Ⅱ）由（1）知的所有取值为：0，1，2，4，5，8.
……………………………………………………………7分
当
时,
的所有取值为(2，3)、(4，3)、(3，2),(3，4)即
；
当
时,的所有取值为(2，2)、(4，4)、(4，2),(2，4)即
…8分
当
时,的所有取值为(1，3)、(3，1)即
；
当
时,的所有取值为(1，2)、(2，1)、(1，4),(4，1)即
…9分
所以的分布列为：
0
1
2
4
5
8
…
…………10分
即的期望
………………12分
19．（本题12分）
解：（I）连接AO，
D1在底面AC的射影是O，
平面AC，…………2分
AO是AD1在平面AC的射影，
底面ABCD为矩形，
AB=2，AD=1，O是CD的中点，
…………4分
（II）过O作
，连接D
则
是二面角D1―AC―D的平面角。…………6分
平面AC，
与平面AC所成的角，
在
…………8分
（III）过C作
于N，
底面ABCD，底面ABCD是矩形。
平面DD1O，
平面ADD1，…………10分
线段CN的长即C到平面ADD1的距离。…………11分
所以C到平面ADD1的距离是
…………12分
解法二（II）：由（I）知OA、OB、OD1两两垂直，以O为坐标原点，直线OA、OB、OD1分别为
轴，建立如图所示的空间直角坐标系
所以
|
…………6分
…………8分
…………12分
得a4=
a3=33.同理可得
符合题意，则
必为与n无关的常数
，得
}为等差数列。 ……………………5分
故
……………………12分
，
，
，
，设P
，则
………………………………………3分
，
，即点P为椭圆短轴端点时，
有最小值－2；
，即点P为椭圆长轴端点时，
：
，A（
），B（
）
，消去
，整理得：
，
得：
或
………7分 ①
……………………………………………8分
，即
，∴
……………………..12分
…………2分 又
…………3分
可化为
的变化情况如下表：
…………6分
为偶函数，
时，