
题目列表(包括答案和解析)
(Ⅰ)(20分)在复数范围内解方程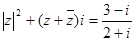 (i为虚数单位)
(i为虚数单位)
(Ⅱ)设z是虚数,ω=z+ 是实数,且-1<ω<2
是实数,且-1<ω<2
(1)求|z|的值及z的实部的取值范围;(10分)
(2)设u=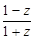 ,求证:u为纯虚数;(5分)
,求证:u为纯虚数;(5分)
(3)求ω-u2的最小值,(5分)
在复数范围内解方程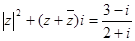 .(i为虚数单位)
.(i为虚数单位)
在复数范围内解方程![]() (i为虚数单位)
(i为虚数单位)
在复数范围内解方程![]() (i为虚数单位).
(i为虚数单位).
①方程2x-5=0在自然数集N中无解;
②方程2x2+9x-5=0在整数集Z中有一解,在有理数集Q中有两解;
③x=i是方程x2+1=0在复数集C中的一个解;
④x4=1在R中有两解,在C中也有两解.
其中正确命题的个数是( )
A.1 B.2 C.3 D.4
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com