
题目列表(包括答案和解析)
设点![]() 动圆P经过点F且和直线
动圆P经过点F且和直线![]() 相切,记动圆的圆心P的轨迹为曲线W。
相切,记动圆的圆心P的轨迹为曲线W。
(1)求曲线W的方程;
(2)过点F作互相垂直的直线![]() ,分别交曲线W于A,B和C,D。求四边形ABCD面积的最小值。
,分别交曲线W于A,B和C,D。求四边形ABCD面积的最小值。
(3)分别在A、B两点作曲线W的切线,这两条切线的交点记为Q。
求证:QA⊥QB,且点Q在某一定直线上。
设点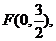 动圆P经过点F且和直线
动圆P经过点F且和直线 相切,记动圆的圆心P的轨迹为曲线W。
相切,记动圆的圆心P的轨迹为曲线W。
(1)求曲线W的方程;
(2)过点F作互相垂直的直线 ,分别交曲线W于A,B和C,D。求四边形ABCD面积的最小值。
,分别交曲线W于A,B和C,D。求四边形ABCD面积的最小值。
(3)分别在A、B两点作曲线W的切线,这两条切线的交点记为Q。
求证:QA⊥QB,且点Q在某一定直线上。
设点 动圆P经过点F且和直线
动圆P经过点F且和直线 相切,记动圆的圆心P的轨迹为曲线W。
相切,记动圆的圆心P的轨迹为曲线W。
(1)求曲线W的方程;
(2)过点F作互相垂直的直线 ,分别交曲线W于A,B和C,D。求四边形ABCD面积的最小值。
,分别交曲线W于A,B和C,D。求四边形ABCD面积的最小值。
(3)分别在A、B两点作曲线W的切线,这两条切线的交点记为Q。
求证:QA⊥QB,且点Q在某一定直线上。
| 3 |
| 2 |
| 3 |
| 2 |
已知函数f(x)=2lnx,g(x)=![]() ax2+3x.
ax2+3x.
(1)设直线x=1与曲线y=f(x)和y=g(x)分别相交于点P、Q,且曲线y=f(x)和y=g(x)在点P、Q处的切线平行,若方程![]() f(x2+1)+g(x)=3x+k有四个不同的实根,求实数k的取值范围;
f(x2+1)+g(x)=3x+k有四个不同的实根,求实数k的取值范围;
(2)设函数F(x)满足F(x)+x[![]() (x)-
(x)-![]() (x)]=-3x2-(a+6)x+1.其中
(x)]=-3x2-(a+6)x+1.其中![]() (x),
(x),![]() (x)分别是函数f(x)与g(x)的导函数;试问是否存在实数a,使得当x∈(0,1]时,F(x)取得最大值,若存在,求出a的取值范围;若不存在,说明理由
(x)分别是函数f(x)与g(x)的导函数;试问是否存在实数a,使得当x∈(0,1]时,F(x)取得最大值,若存在,求出a的取值范围;若不存在,说明理由
一、选择题(每小题5分,共60 )
DCAAD BCBAB CB
二、填空题(每小题4分,共16分)
13.100 14.0 15.  16.B
16.B
三、解答题
17.
解
:
18.解:(Ⅰ)掷出点数x可能是:1,2,3,4.
则 分别得:
分别得: 。于是
。于是 的所有取值分别为:0,1,4 .
的所有取值分别为:0,1,4 .
因此 的所有取值为:0,1,2,4,5,8. …………………………………………2分
的所有取值为:0,1,2,4,5,8. …………………………………………2分
当 且
且 时,
时, 可取得最大值8,
可取得最大值8,
此时, ;
………………………………………………………4分
;
………………………………………………………4分
当 时且
时且 时,
时, 可取得最小值 0.
可取得最小值 0.
此时 …………………………………………………………6分
…………………………………………………………6分
(Ⅱ)由(1)知 的所有取值为:0,1,2,4,5,8.
的所有取值为:0,1,2,4,5,8.
 ……………………………………………………………7分
……………………………………………………………7分
当 时,
时, 的所有取值为(2,3)、(4,3)、(3,2),(3,4)即
的所有取值为(2,3)、(4,3)、(3,2),(3,4)即 ;
;
当 时,
时, 的所有取值为(2,2)、(4,4)、(4,2),(2,4)即
的所有取值为(2,2)、(4,4)、(4,2),(2,4)即 …8分
…8分
当 时,
时, 的所有取值为(1,3)、(3,1)即
的所有取值为(1,3)、(3,1)即 ;
;
当 时,
时, 的所有取值为(1,2)、(2,1)、(1,4),(4,1)即
的所有取值为(1,2)、(2,1)、(1,4),(4,1)即 …9分
…9分
所以 的分布列为:
的分布列为:

0
1
2
4
5
8







…
…………10分
即 的期望
的期望 ………………12分
………………12分
19.(本题12分)
解:(I)连接AO, D1在底面AC的射影是O,
D1在底面AC的射影是O,
 平面AC,…………2分
平面AC,…………2分
 AO是AD1在平面AC的射影,
AO是AD1在平面AC的射影,
 底面ABCD为矩形,
底面ABCD为矩形,
AB=2,AD=1,O是CD的中点,

 …………4分
…………4分
(II)过O作 ,连接D
,连接D

则 是二面角D1―AC―D的平面角。…………6分
是二面角D1―AC―D的平面角。…………6分
 平面AC,
平面AC,

 与平面AC所成的角,
与平面AC所成的角,

在


 …………8分
…………8分
(III)过C作 于N,
于N,
 底面ABCD,底面ABCD是矩形。
底面ABCD,底面ABCD是矩形。
 平面DD1O,
平面DD1O,

 平面ADD1,…………10分
平面ADD1,…………10分
 线段CN的长即C到平面ADD1的距离。…………11分
线段CN的长即C到平面ADD1的距离。…………11分


所以C到平面ADD1的距离是 …………12分
…………12分
解法二(II):由(I)知OA、OB、OD1两两垂直,以O为坐标原点,直线OA、OB、OD1分别为 轴,建立如图所示的空间直角坐标系
轴,建立如图所示的空间直角坐标系 所以
所以
|