
题目列表(包括答案和解析)
等式的基本性质:
(1)等式的两边都________(或________)同一个数或同一个整式,所得结果仍是等式,即如果a=b,那么a±c=b±C.
(2)等式的两边都________(或________)同一个数(除数不能为________),所得结果仍是等式,即如果a=b,那么ac=bc,![]() =
=![]() (c≠0).
(c≠0).
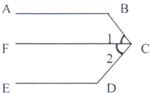 29、如图,根据图形填空:
29、如图,根据图形填空:
 如图,已知AB∥CD,∠E=90°,那么∠B+∠D等于多少度?为什么?
如图,已知AB∥CD,∠E=90°,那么∠B+∠D等于多少度?为什么?湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com