（本小题满分8分）

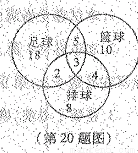
一个学校的足球队、篮球队和排球队分别有28,22,17名成员，一些成员不止参加一支球队，具体情况如图所示，随机选取的一名成员：

（1）      属于不止1支球队的概率是多少？

（2）      属于不超过2支球队的概率是多少？

   

 

某学校课题小组为了研究学生的数学成绩与物理成绩之间的关系，随机抽取高二年级20名学生某次考试成绩（满分100分）如下表所示：

序号	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19	20
数学成绩	95	75	80	94	92	65	67	84	98	71	67	93	64	78	77	90	57	83	72	83
物理成绩	90	63	72	87	91	71	58	82	93	81	77	82	48	85	69	91	61	84	78	86

若单科成绩85分以上（含85分），则该科成绩为优秀．
（1）根据上表完成下面的2×2列联表（单位：人）：

	数学成绩优秀	数学成绩不优秀	合计
物理成绩优秀
物理成绩不优秀
合计			20

（2）根据题（1）中表格的数据计算，有多大的把握，认为学生的数学成绩与物理成绩之间有关系？
（3）若从这20个人中抽出1人来了解有关情况，求抽到的学生数学成绩与物理成绩至少有一门不优秀的概率．
参考数据：
①假设有两个分类变量X和Y，它们的值域分别为{x₁，x₂}和{y₁，y₂}，其样本频数列联表（称为2×2列联表）为：

	y1	y2	合计
x1	a	b	a+b
x2	c	d	c+d
合计	a+c	b+d	a+b+c+d

则随机变量K2=

n(ad-bc)2

(a+b)(c+d)(a+c)(b+d)

，其中n=a+b+c+d为样本容量；
②独立检验随机变量K²的临界值参考表：

P（K2≥k0）	0.50	0.40	0.25	0.15	0.10	0.05	0.025	0.010	0.005	0.001
k0	0.455	0.708	1.323	2.072	2.706	3.841	5.024	6.635	7.879	10.828

（本小题满分12分）

第8届中学生模拟联合国大会将在本校举行，为了搞好接待工作，组委会招募了12名男志愿者和18名女志愿者．将这30名志愿者的身高编成如下茎叶图（单位：cm）：

                       男             女

                               15    7  7  8  9  9  9

9  8   16    0  0  1  2  4  5  8  9

8  6  5  0   17    2  5  6

7  4  2  1   18    0 

1  0   19

若男生身高在180cm以上（包括180cm）定义为“高个子”， 在180cm以下（不包括180cm）定义为“非高个子”， 女生身高在170cm以上（包括170cm）定义为“高个子”，在170cm以下（不包括170cm）定义为“非高个子”．

（1）如果用分层抽样的方法从“高个子”和“非高个子”中抽取6人，则应分别抽取“高个子”、“非高个子”各几人？

（2）从（1）中抽出的6人中选2人担任领座员，那么至少有一人是“高个子”的概率是多少？

 

（本题满分12分）为了了解某年段1000名学生的百米成绩情况，随机抽取了若

干学生的百米成绩，成绩全部介于13秒与18秒之间，将成绩按如下方式分成五组：第一组

[13，14）；第二组[14，15）;……;第五组[17，18].按上述分组方法得到的频率分布直方图如

图所示，已知图中从左到右的前3个组的频率之比为3∶8∶19，且第二组的频数为8.

（1）将频率当作概率，请估计该年段学生中百米成绩在[16，17）内的人数；

（2）求调查中随机抽取了多少个学生的百米成绩；

（3）若从第一、五组中随机取出两个成绩，求这两个成绩的差的绝对值大于1秒的概率.