
题目列表(包括答案和解析)
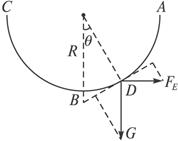
图4-2-16
两位同学是这样求出小球的最大速度的:
甲同学:B是轨道的最低点,小球过B点时速度最大,小球运动过程机械能守恒,mgR=![]() mv2,解得小球在滑动过程中的最大速度为v=
mv2,解得小球在滑动过程中的最大速度为v=![]() .
.
乙同学:B是轨道的最低点,小球过B点时速度最大,小球在B点受到轨道的支持力为N=2mg.由牛顿第二定律有FN-mg=m![]() ,解得球在滑动过程中的最大速度为v=
,解得球在滑动过程中的最大速度为v=![]() .
.
请分别指出甲、乙同学的分析是否正确,若有错,将最主要的错误指出来,解出正确的答案,并说明电场的方向.
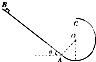 如图所示,与水平面成θ=37°的粗糙斜面与一光滑圆轨道相切于A点,斜面AB的长度s=2.3m,动摩擦因数μ=0.5,圆轨道半径为R=0.6m.让质量为m=1kg物体(可视为质点)从B点以某一沿斜面向下的初速度释放,恰能沿轨道运动到圆轨道的最高点C,空气阻力忽略不计.(取sin37°=0.6,cos37°=0.8)
如图所示,与水平面成θ=37°的粗糙斜面与一光滑圆轨道相切于A点,斜面AB的长度s=2.3m,动摩擦因数μ=0.5,圆轨道半径为R=0.6m.让质量为m=1kg物体(可视为质点)从B点以某一沿斜面向下的初速度释放,恰能沿轨道运动到圆轨道的最高点C,空气阻力忽略不计.(取sin37°=0.6,cos37°=0.8)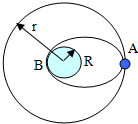 开普勒在1609-1619年发表了著名的开普勒行星三定律,其中第三定律的内容:所有行星在椭圆轨道的半长轴的三次方跟公转周期的平方的比值都相等.实践证明.开普勒三定律也适用于人造地球卫星.2005年10月17日,“神舟”六号飞船在绕地球飞行5天后顺利返回.“神舟”六号飞船在圆轨道正常运行时,其圆轨道半径为r,返回过程可简化为:圆轨道上飞船,在适当位置开动制动发动机一小段时间(计算时可当作一瞬时),使飞船速度减小,并由圆轨道转移到与地面相切的椭圆轨道上,如图所示,椭圆轨道与地面的切点即为设在内蒙的飞船主着陆场,设地球半径为R,地球表面的重力加速度为g,圆轨道为椭圆轨道的一种特殊情况,空气阻力不计.问:
开普勒在1609-1619年发表了著名的开普勒行星三定律,其中第三定律的内容:所有行星在椭圆轨道的半长轴的三次方跟公转周期的平方的比值都相等.实践证明.开普勒三定律也适用于人造地球卫星.2005年10月17日,“神舟”六号飞船在绕地球飞行5天后顺利返回.“神舟”六号飞船在圆轨道正常运行时,其圆轨道半径为r,返回过程可简化为:圆轨道上飞船,在适当位置开动制动发动机一小段时间(计算时可当作一瞬时),使飞船速度减小,并由圆轨道转移到与地面相切的椭圆轨道上,如图所示,椭圆轨道与地面的切点即为设在内蒙的飞船主着陆场,设地球半径为R,地球表面的重力加速度为g,圆轨道为椭圆轨道的一种特殊情况,空气阻力不计.问:如图所示,与水平面成θ=37°的粗糙斜面与一光滑圆轨道相切于A点,斜面AB的长度s=2.3 m,动摩擦因数μ=0.5,圆轨道半径为R=0.6m。让质量为m=1kg物体(可视为质点)从B点以某一沿斜面向下的初速度释放,恰能沿轨道运动到圆轨道的最高点C,空气阻力忽略不计。(取sin37°=0.6,cos37°=0.8)
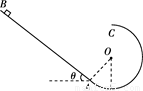
(1)求释放时的初动能;
(2)设物体从C点落回斜面AB上的P点,试通过计算判断P位置比圆心O高还是低.
如图所示,与水平面成θ=37°的粗糙斜面与一光滑圆轨道相切于A点,斜面AB的长度s=2.3 m,动摩擦因数μ=0.5,圆轨道半径为R=0.6m。让质量为m=1kg物体(可视为质点)从B点以某一沿斜面向下的初速度释放,恰能沿轨道运动到圆轨道的最高点C,空气阻力忽略不计。(取sin37°=0.6,cos37°=0.8)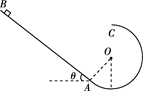
(1)求释放时的初动能;
(2)设物体从C点落回斜面AB上的P点,试通过计算判断P位置比圆心O高还是低.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com