题目列表(包括答案和解析)
如图甲所示，两根足够长的平行导轨处在与水平方向成θ角的斜面上，θ=370，导轨电阻不计，间距L=0.3m．在斜面上加有磁感应强度B=1T、方向垂直于导轨平面向上的匀强磁场．导轨底端接一个阻值R=1Ω的电阻．质量m=1kg、电阻r=2Ω的金属棒ab横跨在平行导轨间，棒与导轨间的动摩擦因数μ=0.5，金属棒从距底端高为h1=2.0m处以平行于导轨向上的初速度v0=10m/s上滑，滑至最高点时高度为h2=3.2m，sin37°=0.6，cos37°=0.8，取g=10m/s2．| 2πm |
| q |
| 4πm |
| q |
| 6 |
| π |
如图15所示，平行金属导轨与水平面间夹角均为θ= 370 ，导轨间距为 lm ，电阻不计，导轨足够长。两根金属棒 ab 和 a’b’的质量都是0.2kg ，电阻都是 1Ω，与导轨垂直放置且接触良好，金属棒a’b’和导轨之间的动摩擦因数为0.5 ，金属棒ab和导轨无摩擦，导轨平面PMKO处存在着垂直轨道平面向上的匀强磁场，导轨平面PMNQ处存在着沿轨道平面向上的匀强磁场，磁感应强度 B 的大小相同．让a’ b’固定不动，将金属棒ab 由静止释放，当 ab 下滑速度达到稳定时，整个回路下滑速度达到稳定时，整个回路消耗的电功率为 18W 。求：
( 1 ) ab 达到的最大速度多大？
( 2) ab 下落了 30m 高度时，其下滑速度已经达到稳定，则此过程中回路电流的发热量 Q 多大？
( 3) 在ab下滑过程中某时刻将 a ' b’固定解除，为确保a ' b’始终保持静止，则a ' b’固定解除时ab棒的速度有何要求？ ( g =10m / s2 , sin370 =0.6 ,cos370 =0.8 )
如图15所示，平行金属导轨与水平面间夹角均为θ= 370 ，导轨间距为 lm ，电阻不计，导轨足够长。两根金属棒 ab 和 a’b’的质量都是0.2kg，电阻都是 1Ω ，与导轨垂直放置且接触良好，金属棒a’b’和导轨之间的动摩擦因数为0.5 ，金属棒ab和导轨无摩擦，导轨平面PMKO处存在着垂直轨道平面向上的匀强磁场，导轨平面PMNQ处存在着沿轨道平面向上的匀强磁场，磁感应强度 B 的大小相同．让a’ b’固定不动，将金属棒ab 由静止释放，当 ab 下滑速度达到稳定时，整个回路下滑速度达到稳定时，整个回路消耗的电功率为 18W 。求 ：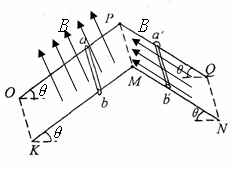
( 1 ) ab 达到的最大速度多大？
( 2) ab 下落了 30m 高度时，其下滑速度已经达到稳定，则此过程中回路电流的发热量 Q 多大？
( 3) 在ab下滑过程中某时刻将 a ' b’固定解除，为确保a ' b’始终保持静止，则a ' b’固定解除时ab棒的速度有何要求？ ( g ="10m" / s2 , sin370 ="0.6" ,cos370 ="0.8" )
如图15所示，平行金属导轨与水平面间夹角均为θ= 370 ，导轨间距为 lm ，电阻不计，导轨足够长。两根金属棒 ab 和 a’b’的质量都是0.2kg，电阻都是 1Ω ，与导轨垂直放置且接触良好，金属棒a’b’和导轨之间的动摩擦因数为0.5 ，金属棒ab和导轨无摩擦，导轨平面PMKO处存在着垂直轨道平面向上的匀强磁场，导轨平面PMNQ处存在着沿轨道平面向上的匀强磁场，磁感应强度 B 的大小相同．让a’ b’固定不动，将金属棒ab 由静止释放，当 ab 下滑速度达到稳定时，整个回路下滑速度达到稳定时，整个回路消耗的电功率为 18W 。求 ：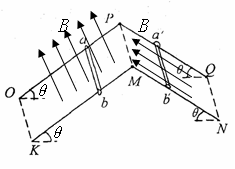
( 1 ) ab 达到的最大速度多大？
( 2) ab 下落了 30m 高度时，其下滑速度已经达到稳定，则此过程中回路电流的发热量 Q 多大？
( 3) 在ab下滑过程中某时刻将 a ' b’固定解除，为确保a ' b’始终保持静止，则a ' b’固定解除时ab棒的速度有何要求？ ( g ="10m" / s2 , sin370 ="0.6" ,cos370 ="0.8" )
一、 选择题：本题共10小题；每小4题分，共40分。
题号
1
2
3
4
5
6
7
8
9
10
答案
C
A
C
A
D
C
B
B
D
B
二、填空题：本题共3小题；共15分。
11、(4分) 分析与解答：原子核变化时如果质量减小（减小的质量称为质量亏损）Dm，根据爱因斯坦质能方程
，可以算出核变释放的能量△E。
答：衰变过程中释放出的能量等于
这个α衰变的方程为： 
说明：本题没给出铀核的质量数，所以用M表示铀核的质量数，这样钍核的质量数为M-4。另外a衰变释放的能表现为a粒子的动能Ea和钍核反冲运动的动能ETh，由于衰变过程动量守恒，则
由于能量守恒，则
解这两个方程可得α粒子的动能
这里的M是衰变前核的质量数。因为M>>4，所以Ea接近DE。
12、(4分) 分析与解答：求媒质中的振动质点在△t时间内通过的路程和末时刻质点相对平衡位置的位移，与质点的初始状态有关，计算比较复杂。但是，如果△t是半周期T／2的整数倍，则计算较为容易，本题则属这种情况。首先，根据题意可求出周期T，以后再求出△t是半周期T／2的多少倍，可进一步计算出△t时间内的路程与末时刻质点相对平衡位置的位移。
因△t=2.5秒，故
=25，则
s=
因为质点M初始时刻在平衡位置，每经过半个周期又回到平衡位置，2.5秒相当于25个半周期，所以末时刻质点又回到平衡位置．
答：在2.5秒的时间内，质点M通过的路程为
说明：时间间隔△t是半周期的整数倍时，又分两种情况．
第一种情况：设△t=nT，那么振动质点在△t时间内通过的路程s=4nA。设初时刻质点相对于平衡位置为Y0，那么末时刻该质点相对于平衡位置的位移Y=Y0。
第二种情况：设△t=（2n+1）T／2，那么振动质点在△t时间内通过的路程s=
13、(7分) 分析与解答：给ab冲量后，ab向右运动， cd受安培力作用而加速，ab受安培力作用而减速。当两者速度相等时，开始共同匀速运动。所以开始时cd的加速度最大，最终cd的速度最大。
以ab为研究对象，设ab的初速度为v0，根据动量定理 I=mv0
以ab、cd系统为研究对象，设ab、cd最终达到的共同速度为v，即cd的末速度vcd，根据系统所受安培力的合力为零，动量守恒
mv0=3mvcd
解得 
又根据在初始时刻ab切割磁感线产生的感应电动势为 E=BLv0
电流
cd所受安培力为 F=BiL
cd的加速度为 
由以上各式得 
系统动能的损失转化为电能，电能又转化为内能．由于ab、cd电阻之比为1∶2，根据Q=I 2Rt∝R，所以cd上产生的电热应该是回路中产生的全部电热的2/3。
因而 
，
。
答：，
，，
三、实验题：本题共3小题；共20分。
14、（6分）分析与解答：
15、( 6分) 分析与解答：根据小灯泡的额定参数，U=6v、P=3w可以计算出小灯泡的额定电流I=
，电压表应选
。
又R灯<<rV而非rA<<R灯，所以采用安培表外接法测小灯泡的电阻R灯。测量时要求电灯两端电压从0V开始连续调节，尽量减小误差，测多组数据。因而滑线变阻器采用分压式接法。
16、(8分) 分析与解答：
(1)(平均速度等于中时刻的即时速度。答数见下表)
(2)见答图；
(3)0.80(注：速度图象的斜率是加速度。答案在0.82～0.78之间均可) 
四、计算题：本题共6小题；共75分。
*17．(11分)分析与解答：
解：（1）货物在传送带上滑行是依靠动摩擦力为动力，即μmg=ma（1）
货物做匀加速运动
由（1）、（2）解出μ=0.375
（2）上述过程中，因传送带始终匀速运动，设它的速度为v对传送带
∴动力对传送带做功为W
=180J
**18、(12分)分析与解答：
解：设稳定状态时，弹簧的伸长为x，物块A在弹力Kx的作用下，做匀速圆周运动。
Kx=mω2(L+x)
因电阻分布均匀，所以阻值与长度成正比。
根据全电路的欧姆定律及分压公式
由以上三式解得
**19．（12分）分析与解答：
解: 根据万有引力是物体沿星球表面做匀速圆周运动的向心力
又知
令 v2=C
由以上三式得
20、(13分)分析与解答：
解：金属棒沿斜面向上运动，切割磁感线，产生的最大感应
力F做功的最大功率P＝Fv=9W
21．(13分)分析与解答：
解：（1）带电粒子从原点射出进入匀强磁场，在垂直于磁场的xoy平面内做匀速圆周运动由左手定则判断磁场的方向垂直于xoy平面指向纸外。从粒子进入电场受电场力作用而速度偏离分析判断：电场强度方向是平行x轴，沿x轴负方向。
半个周期，即：
力作用而做曲线运动，（相当于平抛运动轨迹）
设匀强电场的场强大小为E，粒子射出电场的速度为V，
射出电场时V与y轴夹角120°，即与－y夹角60°
由⑤、⑥、⑦、⑧、⑨解出 
22．(14分)分析与解答：
解：（1）以A、B整体为研究对象，从A与C碰后至AB有共同速度v，系统动量守恒
（2）以A为研究对象，从与C碰后至对地面速度为零，受力为f，位移为s即最大位移．
即三次碰撞后B可脱离A板．
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com