
题目列表(包括答案和解析)
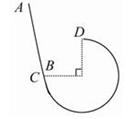
如图所示,倾斜轨道AC与有缺口的圆轨道BCD相切于C,圆轨道半径为R,两轨道在同一竖直平面内,D是圆轨道的最高点,缺口DB所对的圆心角为90°,把一个小球从斜轨道上某处由静止释放,它下滑到C点后便进入圆轨道,要想使它上升到D点后再落到B点,不计摩擦,则下列说法正确的是( )
A..释放点须与D点等高
B..释放点须比D点高R/4
C..释放点须比D点高R/2
D..使小球经D点后再落到B点是不可能的
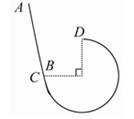
如图所示,倾斜轨道AC与有缺口的圆轨道BCD相切于C,圆轨道半径为R,两轨道在同一竖直平面内,D是圆轨道的最高点,缺口DB所对的圆心角为90°,把一个小球从斜轨道上某处由静止释放,它下滑到C点后便进入圆轨道,要想使它上升到D点后再落到B点,不计摩擦,则下列说法正确的是( )
A.释放点须与D点等高 B.释放点须比D点高R/4
C.释放点须比D点高R/2 D.使小球经D点后再落到B点是不可能的
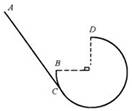
如图所示,倾斜轨道AC与有缺口的圆轨道BCD相切于C,圆轨道半径为R,两轨道在同一竖直平面内,D是圆轨道的最高点,缺口DB所对的圆心角为90°,把一个小球从斜轨道上某处由静止释放,它下滑到C点后便进入圆轨道,想要使它上升到D点后再落到B点,不计摩擦,则下列说法正确的是 ( )
A.释放点须与D点等高
B.释放点须比D点高R/4
C.释放点须比D点高R/2
D.使小球经D点后再落到B点是不可能的
| A.释放点须与D点等高 | ||
B.释放点须比D点高
| ||
C.释放点须比D点高
| ||
| D.使小球经D点后再落到B点是不可能的 |
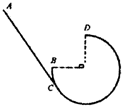
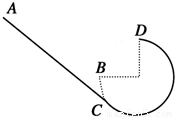 如图所示,倾斜轨道AC与有缺口的圆轨道BCD相切于C,圆轨道半径为R,两轨道在同一竖直平面内,D是圆轨道的最高点,缺口DB所对的圆心角为90°,把一个小球从斜轨道上某处由静止释放,它下滑到C点后便进入圆轨道,要想使它上升到D点后再落到B点,不计摩擦,则下列说法正确的是( )
如图所示,倾斜轨道AC与有缺口的圆轨道BCD相切于C,圆轨道半径为R,两轨道在同一竖直平面内,D是圆轨道的最高点,缺口DB所对的圆心角为90°,把一个小球从斜轨道上某处由静止释放,它下滑到C点后便进入圆轨道,要想使它上升到D点后再落到B点,不计摩擦,则下列说法正确的是( )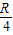
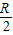
一、选择题:
题号
1
2
3
4
5
6
7
8
9
10
答案
B
C
D
AB
AC
D
CD
AB
B
D
二、实验题:
11、0.874;1.88;9.75
12、(1)  ;
; ; 0 ;
; 0 ;
 ;
;
(2)①让球A多次从同一位置摆下,求B球落点的平均位置;②
 角取值不要太小;
角取值不要太小;
③两球A、B质量不要太小;④球A质量要尽量比球B质量大
三、计算题:
13、f=6000N,P=120000w
14、(1)对平板车施加恒力F后,平板车向右做匀减速直线运动,车向左的加速度大小为
a= m/s2
m/s2
小球到达左端A时,车向右的位移 s= =
=
此时车向右的速度 v1= =
=
小球到达左端A所用时间设为t1,则 =0.5s
=0.5s
小球离开车后做自由落体运动,设下落时间为t2 ,则 h=
|