
题目列表(包括答案和解析)
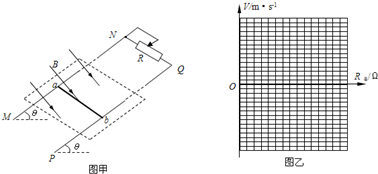 如图甲所示,两根光滑的金属导轨MN、PQ彼此平行,相距L=0.5m,与水平面成θ=37°角放置,在导轨的上部接有一滑动变阻器,其最大阻值R=10Ω.一根质量为m=50g、电阻r=2Ω的直导体棒ab与导轨垂直放置且与导轨接触良好.在图示的矩形虚线区域内存在着垂直导轨平面向下、磁感应强度B=2T的匀强磁场,该磁场始终以速度v0在矩形虚线区域内沿着导轨匀速向上运动.当滑片滑至滑动变阻器的中点时,导体棒恰能在导轨上静止不动.金属导轨的电阻不计,运动的过程中总能保证金属棒处于磁场中.设轨道足够长,重力加速度g取10m/s2,sin37°=0.6,cos37°=0.8.
如图甲所示,两根光滑的金属导轨MN、PQ彼此平行,相距L=0.5m,与水平面成θ=37°角放置,在导轨的上部接有一滑动变阻器,其最大阻值R=10Ω.一根质量为m=50g、电阻r=2Ω的直导体棒ab与导轨垂直放置且与导轨接触良好.在图示的矩形虚线区域内存在着垂直导轨平面向下、磁感应强度B=2T的匀强磁场,该磁场始终以速度v0在矩形虚线区域内沿着导轨匀速向上运动.当滑片滑至滑动变阻器的中点时,导体棒恰能在导轨上静止不动.金属导轨的电阻不计,运动的过程中总能保证金属棒处于磁场中.设轨道足够长,重力加速度g取10m/s2,sin37°=0.6,cos37°=0.8.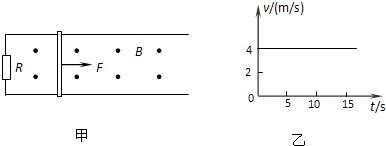 求:
求: 如图甲所示,两根足够长的平行光滑金属导轨固定放置在水平面上,间距L=0.2m,一端通过导线与阻值为R=1Ω的电阻连接;导轨上放一质量为m=0.5kg的金属杆,金属杆与导轨的电阻均忽略不计.整个装置处于竖直向上的大小为B=0.5T的匀强磁场中.现用与导轨平行的拉力F作用在金属杆上,金属杆运动的v-t图象如图乙所示.(取重力加速度g=10m/s2)求:
如图甲所示,两根足够长的平行光滑金属导轨固定放置在水平面上,间距L=0.2m,一端通过导线与阻值为R=1Ω的电阻连接;导轨上放一质量为m=0.5kg的金属杆,金属杆与导轨的电阻均忽略不计.整个装置处于竖直向上的大小为B=0.5T的匀强磁场中.现用与导轨平行的拉力F作用在金属杆上,金属杆运动的v-t图象如图乙所示.(取重力加速度g=10m/s2)求:

一、单项选择题:本题共5小题,每小题3分,共15分
题 号
1
2
3
4
5
答 案
D
D
B
C
A
二、多项选择题:本题共4小题,每小题4分,共16分.每题有多个选项符合题意,全部选对的得4分,选对但不全的得2分,错选或不答的得0分.
题 号
6
7
8
9
答 案
AC
AD
ABC
CD
三、简答题:本题分必做题(第10、11题)和选做题(第12题)两部分,共计42分.请将解答填在答题卡相应的位置.
10、⑴ a/宿迁市2009届高三物理模拟试题2.files/image062.gif) b ⑵ 变大 ⑶4.4
b ⑵ 变大 ⑶4.4
11、/宿迁市2009届高三物理模拟试题2.files/image064.gif) a~m′
3kg
1.5 kg
a~m′
3kg
1.5 kg
12.选做题(请从A、B和C三小题中选定两小题作答,并在答题卡上把所选题目对应字母后的方框涂满涂黑.如都作答则按A、B两小题评分.)
A. (选修模块3-3) (12分)
⑴CD ⑵低 1/2 ⑶0.07Kg
B. (选修模块3-4) (12分)
⑴图略 0.245τ2 9.47 ⑵BC ⑶200m 53°
C. (选修模块3-5) (12分)
⑴AD ⑵①BD ②/宿迁市2009届高三物理模拟试题2.files/image066.gif)
四、计算题:本题共3小题,共47分.解答时请写出必要文字说明、方程式和重要的演算步骤.只写出最后答案的不能得分.有数值计算的题,答案中须明确写出数值和单位.
13.(1)由动能定理,得
qU=mv02-0 ……① ∴v0=……… ②
(2)粒子从A1点进入磁场后,在磁场中运动了四分之一周期后从B点出磁场,轨迹圆心为O1,速度方向改变了900,∵AC=0.6R,∴O点到A1O1距离为0.8R,
△OO1A≌△OO1B,∠A1O1O=∠BO1O=450,轨迹半径
r=0.6R+0.8R=1.4R……………③
由牛顿定律,得
qv0B = mv02/r……………④ ∴B = …………⑤
(3)电场中运动的时间为
t1 = = ……………⑥
在AA1之间做匀速直线运动,时间为
t2 = = ……………⑦
在磁场中运动,时间为
t3= =/宿迁市2009届高三物理模拟试题2.files/image068.gif) =
=/宿迁市2009届高三物理模拟试题2.files/image070.gif) ………………-⑧
………………-⑧
粒子从开始运动到出磁场过程的总时间
/宿迁市2009届高三物理模拟试题2.files/image071.gif) t = t1+t2+t3
= + +
t = t1+t2+t3
= + +/宿迁市2009届高三物理模拟试题2.files/image070.gif)
14.(1)本题要求小球停在O点或O点左方,必有:
/宿迁市2009届高三物理模拟试题2.files/image074.gif) 即:
即:/宿迁市2009届高三物理模拟试题2.files/image076.gif) 此为μ的上限
此为μ的上限
设小球到达左方最远点距O点的距离为/宿迁市2009届高三物理模拟试题2.files/image078.gif) ,因最后停止点不能越过O点,满足:
,因最后停止点不能越过O点,满足:
/宿迁市2009届高三物理模拟试题2.files/image080.gif) ……………………………②
……………………………②
因B为最远点有:
/宿迁市2009届高三物理模拟试题2.files/image082.gif) ………………………②
………………………②
得:/宿迁市2009届高三物理模拟试题2.files/image084.gif)
代入(1)得:/宿迁市2009届高三物理模拟试题2.files/image086.gif)
令:/宿迁市2009届高三物理模拟试题2.files/image088.gif)
得:/宿迁市2009届高三物理模拟试题2.files/image090.gif)
/宿迁市2009届高三物理模拟试题2.files/image092.gif)
由此中知μ的取值范围为:/宿迁市2009届高三物理模拟试题2.files/image094.gif)
(2)要让小球在左方最远点B处停处,则必有:
/宿迁市2009届高三物理模拟试题2.files/image096.gif) ……………………………③
……………………………③
由②③得/宿迁市2009届高三物理模拟试题2.files/image098.gif)
15.(1)释放小球A前,物体B处于平衡状态,
/宿迁市2009届高三物理模拟试题2.files/image100.gif) 得
得/宿迁市2009届高三物理模拟试题2.files/image102.gif) 故弹簧被拉长了
故弹簧被拉长了
(2)小球从杆顶端运动到C点的过程,由动能定理:
/宿迁市2009届高三物理模拟试题2.files/image104.gif) ①
①
其中/宿迁市2009届高三物理模拟试题2.files/image106.gif)
而/宿迁市2009届高三物理模拟试题2.files/image108.gif)
物体B下降的高度/宿迁市2009届高三物理模拟试题2.files/image110.gif) ②
②
由此可知,此时弹簧被压缩了
再以A、B和弹簧为系统,由机械能守恒:
/宿迁市2009届高三物理模拟试题2.files/image112.gif) ③
③
对小球进行速度分解可知,小球运动到C点时物体B的速度/宿迁市2009届高三物理模拟试题2.files/image114.gif) ④
④
由①②③④联立可得:
/宿迁市2009届高三物理模拟试题2.files/image116.gif)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com