题目列表(包括答案和解析)
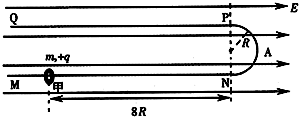如图所示的竖直平面内有范围足够大、水平向右的匀强电场，一绝缘轨道由两段直杆和一半径为R的半圆环组成，固定在纸面所在的竖直平面内．直杆MN、PQ水平且足够长，MNAP段是光滑的（其中A点是半圆环的中点），PQ段是粗糙的．现有一质量为m、带电+q的小环甲（可视为质点）套在MN杆上，它所受电场力为其重力的0.5倍．将小环甲从N点左侧8R处由静止开始释放，如图，且知小环甲与直杆PQ间的动摩擦因数为μ（μ＜0.5，且最大静摩擦力与滑动摩擦力大小相等），求：如图甲所示，光滑且足够长的平行金属导轨MN、PQ固定在同一水平面上，两导轨间距L=0.2m，导轨电阻忽略不计，其间连接有固定电阻R=1Ω。导轨上放一质量m=0.1kg、电阻r=0.5Ω的金属杆ab，整个装置处于磁感应强度B=0.5T的匀强磁场中，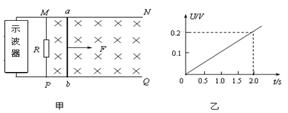
磁场方向竖直向下。现用一与导轨平面平行且与ab垂直的外力F拉金属杆ab，使之由静止开始向右运动，将R两端的电压U输入示波器，获得电压U随时间t变化的关系如图乙所示。
（1）求金属杆的加速度大小
（2）求第2s末F的瞬时功率
（3）F作用到2s时撤去，求撤去F后定值电阻R上产生焦耳热的最大值
甲 乙
（1）若弹簧的劲度系数为k＝200 N/m，以作用力F为纵坐标，物块A移动的距离为横坐标，试通过定量计算在图乙的坐标系中画出推力F随物块A位移的变化图线。
（2）求弹簧储存的弹性势能E0的大小。
（3）当物块B缓慢地向右移动了
(1)将小环甲从N点左侧8R处由静止开始释放，且知小环甲与直杆PQ间的动摩擦因数为μ(μ＞0.5，且最大静摩擦力与滑动摩擦力大小相等)，求小环甲在水平杆PQ上通过的路程.
图13a
(2)若另一质量也为m、不带电的绝缘小环乙(视为质点)套在MN杆上的N点，如图13b所示，现从NM杆上的D点由静止释放小环甲，小环甲此后与乙碰撞时间极短，且碰后瞬间两者速度相同但不粘连，乙环沿NAP运动到P点时刚好停止，求DN间的距离x0.
图13b
质量为20Kg的物体在动摩擦因数为0.1的水平面上向左运动，在运动过程中受到水平向左，大小为10N的拉力作用，则物体受到的加速度为一、选择题：选对的给6分，选错的得0分。
1．B 2．D 3．B 4．B 5．D
6．A 7．D 8．A 9．D 10．D 11． C 12．D
二、选择题：全部选对的给6分，选对但不全的给3分，有选错的得0分。
13．BC 14．C 15．A 16．A 17．D 18．AC
19．（1）(12分)①0.04 左； ② 1.215 9.375
(2) (6分)
．
③ 单向导电性
20. 
(15分)（1）如图所示：（3分）
（2）当ab杆速度为v时，感应电动势E=BLv，（2分）
此时电路电流 
（2分）
ab杆受到安培力
（3分）
根据牛顿运动定律，有
（3分）
解得
（2分）
21．（19分）
22．（20分）
解：（1）只有磁场时，电子作圆周运动，
轨迹如图所示，利用几何作图，O’是其圆心，
（2）只有电场时，电子从MN上的D点离开电场，如图所示，设D点横坐标为x
（3）从A点到D点，电场力做正功，由动能定理得：
23、（共15分）（1）氧（1分）
（2） （2分）；N2 H 4−4e− +4OH−= N 2 +4H2O（2分）
（3）2Cl−−2e−=Cl2↑（2分），升高（2分）；
（4）①NH4Cl（或NH4NO3）（2分），NaOH；（2分）
②c(Cl−)＞c(NH4+)＞c(Na+)＞c(OH−)＞c(H+)或c(NO3−)＞c(NH4+)＞c(Na+)＞c(OH−)＞c(H+)
（2分）
24、（14分，每空2分）
Ⅰ、 ⑴ S2- + H2O
HS- +OH-
；HS- + H2OH2S +OH-；
⑵ 2.7×10-3 ； ⑶ +172.5 ；
Ⅱ、（1）K＝； 放热。 (2）1.5×10－3mol/(L?s)。 (3） c。
25．（16分）（1）KClO3（2分）… H2O2（2分）
|