
题目列表(包括答案和解析)
已知函数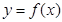 的定义域为
的定义域为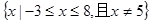 ,值域为
,值域为 .下列关于函数
.下列关于函数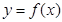 的说法:①当
的说法:①当 时,
时, ;②点
;②点 不在函数
不在函数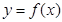 的图象上;③将
的图象上;③将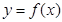 的图像补上点(5,0),得到的图像必定是一条连续的曲线;④
的图像补上点(5,0),得到的图像必定是一条连续的曲线;④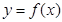 的图象与坐标轴只有一个交点.其中一定正确的说法的个数是( )
的图象与坐标轴只有一个交点.其中一定正确的说法的个数是( )
A. 1 B. 2 C. 3 D. 4
函数![]() 的定义域为(0,1](
的定义域为(0,1](![]() 为实数).
为实数).
⑴当![]() 时,求函数
时,求函数![]() 的值域;
的值域;
⑵若函数![]() 在定义域上是减函数,求
在定义域上是减函数,求![]() 的取值范围;
的取值范围;
⑶求函数![]() 在x∈(0,1]上的最大值及最小值,并求出函数取最值时
在x∈(0,1]上的最大值及最小值,并求出函数取最值时![]() 的值
的值
函数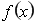 的定义域为
的定义域为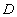 ,若存在闭区间
,若存在闭区间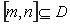 ,使得函数
,使得函数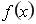 满足以下两个条件:(1)
满足以下两个条件:(1) 在[m,n]上是单调函数;(2)
在[m,n]上是单调函数;(2) 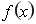 在[m,n]上的值域为[2m,2n],则称区间[m,n]为
在[m,n]上的值域为[2m,2n],则称区间[m,n]为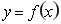 的“倍值区间”.下列函数中存在“倍值区间”的有 (填上所有正确的序号)
的“倍值区间”.下列函数中存在“倍值区间”的有 (填上所有正确的序号)
①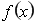 =x2(x≥0); ②
=x2(x≥0); ②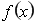 =ex(x∈R);
=ex(x∈R);
③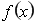 =
=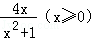 ;④
;④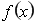 =
=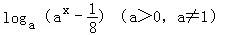 .
.
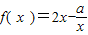 的定义域为(0,1](a为实数).
的定义域为(0,1](a为实数).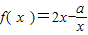 的定义域为(0,1](a为实数).
的定义域为(0,1](a为实数).一、选择题:本大题共有12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项正确的
题号
1
2
3
4
5
6
7
8
9
10
11
12
答案
C
D
C
D
D
A
B
B
C
B
A
C
二、填空题:本大题共4小题,每小题4分,共16分,把答案填在答题卡的相应位置。
13.(1,0) 14. 15.1 16.②③
15.1 16.②③
三、解答题:本大题共6小题,共74分。解答应写出文字说明,证明过程或演算步骤。
17.(本小题满分12分)
解:(Ⅰ)由


 ……………………………………4分
……………………………………4分
又因为
解得 …………………………………………5分
…………………………………………5分
 ………………………………………6分
………………………………………6分
(Ⅱ)在 ,
,

 。……………………………………………9分
。……………………………………………9分
 ,
,
即
 ,
,
又由(Ⅰ)知
故 取得最大值时,
取得最大值时, 为等边三角形. …………………………12分
为等边三角形. …………………………12分
 18.(本小题满分12分)
18.(本小题满分12分)
解:(Ⅰ)设抽取的样本为 名学生的成绩,
名学生的成绩,
则由第一行中可知
 ;
;
②处的数值为 ;
;
③处的数值为 …………4分
…………4分
(Ⅱ)成绩在[70,80 分的学生频率为0.2,成绩在[80.90
分的学生频率为0.2,成绩在[80.90 分的学生频率为0.32,
分的学生频率为0.32,
所以成绩在[70.90 分的学生频率为0.52,……………………………………6分
分的学生频率为0.52,……………………………………6分
由于有900名学生参加了这次竞赛,
所以成绩在[70.90 分的学生约为
分的学生约为 (人)………………8分
(人)………………8分
(Ⅲ)利用组中值估计平均为
 …………12分
…………12分
19.(本小题满分12分)
解:(I)由几何体的三视图可知,低面ABCD是边长为4的正方形,
 ,…………………………………3分
,…………………………………3分
且 ,
,
 ………………6分
………………6分
 (Ⅱ)连
(Ⅱ)连 ,
,
 ,
,
 °
°

 °
°
 ………………10分
………………10分
又

 ……………………………………………………………………12分
……………………………………………………………………12分
20.(本小题满分12分)
解:(I)10年后新建住房总面积为
 。………………………3分
。………………………3分
设每年拆除的旧住房为 ………………5分
………………5分
解得 ,即每年拆除的旧住房面积是
,即每年拆除的旧住房面积是 …………………………………6分
…………………………………6分
(Ⅱ)设第 年新建住房面积为
年新建住房面积为 ,则
,则 =
=
所以当 ;…………………………………………9分
;…………………………………………9分
当


故 ……………………………………12分
……………………………………12分
21.(本小题满分12分)
解:(Ⅰ)由题意可知,可行域是以 为顶点的三角形,因为
为顶点的三角形,因为 ,
,
故 ,
,
 为直径的圆,
为直径的圆,
故其方程为 ………………………………………………3分
………………………………………………3分
设椭圆 的方程为
的方程为 ,
,

又 .
.
故椭圆 ………………………………………5分
………………………………………5分
(Ⅱ)直线 始终与圆
始终与圆 相切。
相切。
设 。
。
当
 。
。
若
 ;
;
若
 ;
;
即当
 ……………………………7分
……………………………7分
当 时,
时, ,
,

 。
。
因此,点Q的坐标为 。
。
 ……………10分
……………10分

当 ,
,
 。
。
综上,当
 ,…………12分
,…………12分
22.(本小题满分14分)
解:(I)(1) ,
,
 。…………………………………………1分
。…………………………………………1分
 处取得极值,
处取得极值,
 …………………………………………………2分
…………………………………………………2分
即
 ………………………………………4分
………………………………………4分
(ii)在
 ,
,
由

 ,
,

 ;
;
当
 ;
;

 ;
;
 .……………………………………6分
.……………………………………6分
面
 ,
,
且
又
 ,
,

 ……………9分
……………9分
(Ⅱ)当 ,
,
① ;
;
②当 时,
时,
 ,
,

③ ,
,
从面得 ;
;
综上得, .………………………14分
.………………………14分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com