给出定义：若函数在D上可导，即存在，且导函数在D上也可导，则称ƒ（x）在D上存在二阶导函数，记，若在D上恒成立，则称ƒ（x）在D上为凸函数，以下四个函数在（0，）上不是凸函数的是（  ）

A. ƒ（x）=sinx+cosx                    B. ƒ（x）=lnx-2x

C. ƒ（x）= -x³+2x-1                     D. ƒ（x）=xe^x

设函数f（x）=在[1，+∞上为增函数.  

（1）求正实数a的取值范围；

（2）比较的大小，说明理由；

（3）求证：（n∈N*, n≥2）

【解析】第一问中，利用

解:（1）由已知：，依题意得：≥0对x∈[1，+∞恒成立

∴ax－1≥0对x∈[1，+∞恒成立    ∴a－1≥0即：a≥1

（2）∵a=1   ∴由（1）知：f（x）=在[1，+∞)上为增函数，

∴n≥2时：f（）=

  

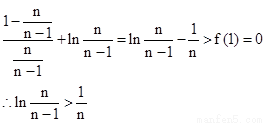
 (3)  ∵   ∴

 

给出定义：若函数f（x）在D上可导，即f′（x）存在，且导函数f′（x）在D上也可导，则称f（x）在D上存在二阶导函数，记f′（x）=（f′（x））′．若f″（x）＜0在D上恒成立，则称f（x）在D上为凸函数．以下四个函数在（0，

π

2

）上不是凸函数的是．（把你认为正确的序号都填上）
①f（x）=sin x+cos x；
②f（x）=ln x-2x；
③f（x）=-x³+2x-1；
④f（x）=xe^x．

A、f（x）=1-sinx

B、f（x）=ex-2x

C、f（x）=x3-x2-1

D、f（x）=-xe-x