题目列表(包括答案和解析)
（1）盒中装有6枝白粉笔和2枝红粉笔，从中任意取出3枝，其中所含白粉笔的枝数ξ；
（2）从4张已编号（1号—4号）的卡片中任意取出2张，被取出的卡片号数之和ξ；
（3）离开天安门的距离η；
（4）袋中有大小完全相同的红球5个，白球4个，从袋中任意取出一球，若取出的球是白球，则过程结束；若取出的球是红球，则将此红球放回袋中，然后重新从袋中任意取出一球……直至取出的球是白球，此约定下的取球次数ξ.
写出下列随机变量的可能取值，并说明随机变量取值所表示的随机试验的结果：
(1)一烟花内装5节起火器，每节起火器与引信相连，每节起火器被点燃烟花就喷出一次火花．若燃放中引信断开，则烟花熄灭，那么这一烟花在点燃引信后可喷出火花的次数；
(2)102路公共汽车每5分钟一趟，一乘客在102路公共汽车的站台上等车的时间；
(3)一粒种子的发芽率为0．7，今埋下5粒种子，发芽种子的粒数；
(4)袋中红球10个，白球5个，从袋中每次任取出一个球，直到取出的球是红球为止的需要的取球次数．
(1)一烟花内装5节起火器，每节起火器与引信相连，每节起火器被点燃烟花就喷出一次火花．若燃放中引信断开，则烟花熄灭，那么这一烟花在点燃引信后可喷出火花的次数；
(2)102路公共汽车每5分钟一趟，一乘客在102路公共汽车的站台上等车的时间；
(3)一粒种子的发芽率为0．7，今埋下5粒种子，发芽种子的粒数；
(4)袋中红球10个，白球5个，从袋中每次任取出一个球，直到取出的球是红球为止的需要的取球次数．
，
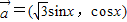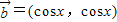，记
．
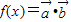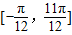的简图，并指出该函数的图象可由y=sinx（x∈R）的图象经过怎样的平移和伸缩变换得到？
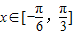时，函数g（x）=f（x）+m的最小值为2，试求出函数g（x）的最大值并指出x取何值时，函数g（x）取得最大值．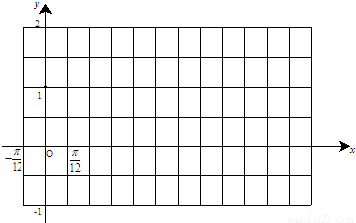
，
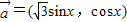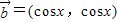，记
．
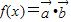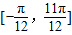的简图，并指出该函数的图象可由y=sinx（x∈R）的图象经过怎样的平移和伸缩变换得到？
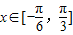时，函数g（x）=f（x）+m的最小值为2，试求出函数g（x）的最大值并指出x取何值时，函数g（x）取得最大值．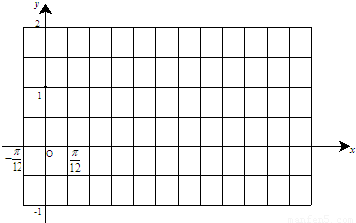
一、选择题
题号
1
2
3
4
5
6
7
8
9
10
11
12
答案
A
D
C
C
B
B
A
B
C
D
C
D
二、填空题
13．2 14．
15．60 16．③④
三、解答题
17．解：（1）
，
（2分）
又
（4分）
. （6分）
（2）
（8分）
（10分）
18．（1）证明：连结
交
于点
，取
的中点
，连结
，则// 
且
依题意，知
且
，
，且
，
故四边形
是平行四边形，
，即
（4分）
又
平面
，
平面， （6分）
（2）延长
交
的延长线于
点，连结
，作
于
点，连结
．
∵平面
平面
，平面
平面
，
平面，
∴
平面
，
由三垂线定理，知
，故
就是所求二面角的平面角．（8分）
∵平面平面，平面平面
平面，故
就是直线与平面成的角， （10分）
知
设
，则
．
在
中：
在
中：由
，
，知
故平面与平面所成的锐二面角的大小为45°． （12分）
19．解：（1）记
表示事无偿援助，“取出的2伯产吕中无二等品”，
表示事件“取出的2件产品中恰有1件是二等品”。则、互斥，且
故
依题意，知
又
，得
（6分）
（2）若该批产品有100件，由（1）知，其中共有二等品100×0．2=20件
记
表示事件“取出的2件产品中无二等品”，则事件
与事件互斥，
依题意，知
故
（12分）
20．解：（1）
在
上单调递增，
上单调递减，
有两根，2，
（6分）
（2）令
则
因为
在
上恒大于0，
所以
，在上单调递增，故
（12分）
21．（1）依题意，知
由
，得
故
，得
4分
（2）依题意，知
由
，得
即
，得
8分
（3）由
、
是相互垂直的单位向量，
知，
得
记数列
的前
项和为
，
则有
相减得，
故
12分
22．解：（1）设
依题意得
（2分）
消去
，
，整理得
． （4分）
当
时，方程表示焦点在
轴上的椭圆；
当
时，方程表示焦点在
轴上的椭圆；
当
时，方程表示圆． （6分）
（2）当
时，方程为
设直线
的方程为
（8分）
消去得
（10分）
根据已知可得
，故有
直线的斜率为
（12分）
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com