
题目列表(包括答案和解析)
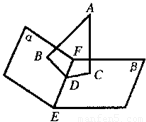
 二面角α-EF-β的大小为120°,A是它内部的一点AB⊥α,AC⊥β,B,C分别为垂足.
二面角α-EF-β的大小为120°,A是它内部的一点AB⊥α,AC⊥β,B,C分别为垂足.二面角α–EF–β的大小为120°,A是它内部的一点AB⊥α,AC⊥β,B,C分别为垂足.
(1)求证:平面ABC⊥β;
(2)当AB=4cm,AC=6cm,求BC的长及A到EF的距离.


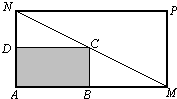 (2008•佛山二模)某物流公司购买了一块长AM=30米、宽AN=20米的矩形地块,规划建设占地如图中矩形ABCD的仓库,其余地方为道路或停车场,要求顶点C在地块对角线MN上,顶点B,D分别在边AM,AN上,设AB长度为x米.
(2008•佛山二模)某物流公司购买了一块长AM=30米、宽AN=20米的矩形地块,规划建设占地如图中矩形ABCD的仓库,其余地方为道路或停车场,要求顶点C在地块对角线MN上,顶点B,D分别在边AM,AN上,设AB长度为x米.一.选择题:
1
2
3
4
5
6
7
8
9
10
11
12
B
D
A
D
C
D
A
C
B
A
C
B
二.填空题:
13. 7 ;14. ;15.
;15.
 ;16①②③④
;16①②③④
三.解答题:
 18. 记第一、二、三次射击命中目标分别为事件A,B,C三次均未命中目标的事件为D.依题意
18. 记第一、二、三次射击命中目标分别为事件A,B,C三次均未命中目标的事件为D.依题意 . 设在
. 设在
 处击中目标的概率为
处击中目标的概率为 ,则
,则 ,由
,由
 时
时 ,所以
,所以 ,
, , 2分
, 2分
 ,
,
 ,
, ,
, .
.
5 分
(Ⅰ)由于各次射击都是独立的,所以该射手在三次射击击中目标的概率为
 ,
,
= . 8分
. 8分
(Ⅱ)依题意,设射手甲得分为 ,则
,则 ,
, ,
,
 ,
, ,所以
,所以 的分布列为
的分布列为

0
1
2
3





所以 。 12分
。 12分

20. (Ⅰ)证明:连结 交
交 于点
于点 ,连结
,连结 .
.
在正三棱柱 中,四边形
中,四边形 是平行四边形,
是平行四边形,
∴ .
.
 ∵
∵ ,
,
∴ ∥
∥ . ………………………2分
. ………………………2分
∵ 平面
平面 ,
, 平面
平面 ,
,
∴ ∥平面
∥平面 . …………………………4分
. …………………………4分
(Ⅱ)过点 作
作 交
交 于
于 ,过点
,过点 作
作 交
交 于
于 ,连结
,连结 .
.
 ∵平面
∵平面
 平面
平面 ,
, 平面
平面 ,平面
,平面 平面
平面 ,
,
∴ 平面
平面 .
.
∴ 是
是 在平面
在平面 内的射影.
内的射影.
∴ .
.
∴ 是二面角
是二面角 的平面角.
的平面角.
在直角三角形 中,
中, .
.
同理可求:  .
.
∴ .
.
∵ ,
,
∴ . …………………………12分
. …………………………12分
21.(Ⅰ) ,令
,令 ,解得
,解得 或
或 ,1分
,1分
当 时,
时, ,
, 为增函数;当
为增函数;当 时
时 ,
, 为减函数;当
为减函数;当 时
时 ,
, 为增函数。4分
为增函数。4分  当
当 时,
时, 取得极大值为-4,当
取得极大值为-4,当 时,
时, 取处极小值为
取处极小值为 。…………………………6分
。…………………………6分
(Ⅱ)设 ,
, 在
在 上恒成立.
上恒成立.
 ,
, ,若
,若 ,显然
,显然 。
8分 若
。
8分 若 ,
,
 ,令
,令 ,解得
,解得 ,或
,或 ,当
,当 时,
时,
 ,当
,当 时,
时, .10分
.10分
 当
当 时,
时, .
.
即 ,解不等式得
,解不等式得 ,
, ,当
,当 时,
时,
 满足题意.综上所述
满足题意.综上所述 的范围为
的范围为 …………...12分
…………...12分


湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com