练习册

  • 练习册
  • 试题
    吉林省延边州2008-2009学年度质量检测 【查看更多】

     

    题目列表(包括答案和解析)

    （本小题12分）试用含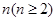的表达式表示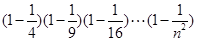的值，并用数学归纳法证明你的结论.

     

    查看答案和解析>>

    （本小题12分）
    已知是等差数列，且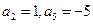
    ①求的通项。
    ②求的前n项和Sn的最大值。

    查看答案和解析>>

    (本小题12分)

    已知,

     (1)判断的奇偶性并用定义证明；

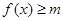    (2)当时，总有成立，求的取值范围.

     

    查看答案和解析>>

    （本小题12分）若数列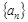的前n 项和Sn满足：Sn= 2an+1.

    （1）求，，；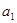

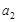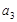    （2）求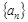的通项公式.

     

    查看答案和解析>>

    （本小题12分）袋中有大小、形状相同的红、黑球各两个，现依次不放回地随机取3次，每次取一个球.

    （1）试问：一共有多少种不同的结果，请列出所有可能的结果；

    （2）若摸到红球时得2分，摸到黑球时得1分，求3次摸球所得总分为5的概率.

     

    查看答案和解析>>

    一.选择题:

    1

    2

    3

    4

    5

    6

    7

    8

    9

    10

    11

    12

    B

    B

    A

    D

    C

    D

    C

    C

    D

    C

    C

    B

    二.填空题:

    13. 1600 ;14.7;15. 14;16①②③④

     

    三.解答题:

    17．(本题满分10分)（Ⅰ）

    （Ⅱ）

    所以的最大值为

    18.记小张能过第一关的事件为A，直接去闯第二关能通过的事件为B，直接去闯第三关能通过的事件为C.      2分

     则P（A）=0.8，P（B）=0.75，P（C）=0.5

    （Ⅰ）小张在第二关被淘汰的概率为P（A?）=P（A）?（1-P（B））

     =0.8×0.25=0.2. 

     答：小张在第二关被淘汰的概率为0.2      7分

    （Ⅱ）小张不能参加决赛的概率为P=1-P（A?B?C）=1-0.8×0.75×0.5=0.7

    答：小张不能参加决赛的概率为0.7.    12分

    19.（Ⅰ）设等差数列的公差为d（d0）.

          成等比数列，

       即，化简得，注意到，，

      6分，

    （Ⅱ）=9，，。。

       12分。

     

    20.（Ⅰ）证明：连结交于点，连结.

    在正三棱柱中，四边形是平行四边形，

    ∴.

    ∵，

    ∴∥.   ……………………………2分

          ∵平面，平面，

    ∴∥平面.       …………………………4分

     

    (Ⅱ）过点作交于，过点作交于，连结.

    ∵平面平面，平面，平面平面，

          ∴平面.

    ∴是在平面内的射影.

    ∴.

    ∴是二面角的平面角.  

           在直角三角形中，.

    同理可求： .

    ∴.

    ∵，

    ∴.          ……………………12分

    21．（Ⅰ），依题意得，即，.        2分   ,, ,    5分

    (Ⅱ）令得.,

    ,.因此,当时,   8分

    要使得不等式对于恒成立,只需.则.故存在最小的正整数,使得不等式

    对于恒成立.

    \

    (Ⅱ）

     

     

     

     


    同步练习册答案