
题目列表(包括答案和解析)
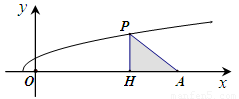
如图,已知点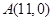 ,函数
,函数 的图象上的动点
的图象上的动点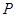 在
在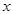 轴上的射影为
轴上的射影为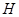 ,且点
,且点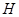 在点
在点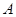 的左侧.设
的左侧.设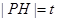 ,
,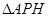 的面积为
的面积为 .
.
(Ⅰ)求函数 的解析式及
的解析式及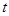 的取值范围;
的取值范围;
(Ⅱ)求函数 的最大值.
的最大值.
已知点![]() 是函数
是函数![]() 的图象上一点,等比数列
的图象上一点,等比数列![]() 的前
的前![]() 项和为
项和为![]() 数列
数列![]() 的首项为
的首项为![]() ,且前
,且前![]() 项和
项和![]() 满足
满足![]()
(1)数列![]() ,
,![]() 的通项公式;
的通项公式;
(2)若数列![]() 的前
的前![]() 项和为
项和为![]() ,问
,问![]() 的最小正整数
的最小正整数![]() 是多少?
是多少?
(09年长沙一中一模理)(13分)已知函数f (x) = lnx,g (x) =![]() (a>0),设F(x) = f (x) + g (x).
(a>0),设F(x) = f (x) + g (x).
![]() (1)求函数F(x)的单调区间;
(1)求函数F(x)的单调区间;
(2)若点![]() 为函数
为函数![]() 的图象上任意一点,当
的图象上任意一点,当![]() 时,点P处的切线的斜率k≤
时,点P处的切线的斜率k≤![]() 恒成立,求实数a的最小值;
恒成立,求实数a的最小值;
(3)是否存在实数m,使得函数y = g(![]() ) + m 1的图象与函数y = f (1 + x2)的图象恰有四个不同的交点?若存在,求出实数m的取值范围;若不存在,说明理由.
) + m 1的图象与函数y = f (1 + x2)的图象恰有四个不同的交点?若存在,求出实数m的取值范围;若不存在,说明理由.
已知点 是函数
是函数 的图象上一点,数列
的图象上一点,数列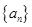 的前n项和
的前n项和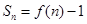 .
.
(Ⅰ)求数列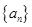 的通项公式;
的通项公式;
(Ⅱ)将数列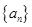 前2013项中的第3项,第6项, ,第3k项删去,求数列
前2013项中的第3项,第6项, ,第3k项删去,求数列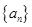 前2013项中剩余项的和.
前2013项中剩余项的和.
已知点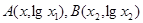 是函数
是函数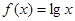 的图象上任意不同两点,依据图象可知,段段AB总是位于A,B两点之间函数图象的下方,因此有结论
的图象上任意不同两点,依据图象可知,段段AB总是位于A,B两点之间函数图象的下方,因此有结论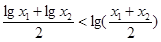 成立。运用类比思想方法可知,若点
成立。运用类比思想方法可知,若点 ,
, 是函数
是函数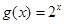 的图象上的不同两点,则类似地有成立 。
的图象上的不同两点,则类似地有成立 。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com