
题目列表(包括答案和解析)
若![]() 是从区间
是从区间![]() 内任取一个实数,
内任取一个实数,![]() 是从区间
是从区间![]() 内任取一个实数,则关于
内任取一个实数,则关于![]() 的一元二次方程
的一元二次方程![]() 有实根的概率为 ( )
有实根的概率为 ( )
A 、![]() B、
B、![]() C、
C、![]() D、
D、![]()
若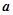 是从区间
是从区间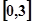 内任取一个实数,
内任取一个实数,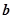 是从区间
是从区间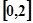 内任取一个实数,则关于
内任取一个实数,则关于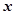 的一元二次方程
的一元二次方程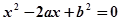 有实根的概率为 ( )
有实根的概率为 ( )
A 、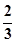 B、
B、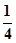 C、
C、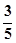 D、
D、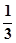
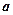 是从区间
是从区间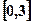 内任取一个实数,
内任取一个实数,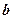 是从区间
是从区间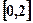 内任取一个实数,则关于
内任取一个实数,则关于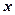 的一元二次方程
的一元二次方程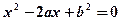 有实根的概率为 ( )
有实根的概率为 ( )A. | B. | C. | D. |
A、
| ||
B、
| ||
C、
| ||
D、
|
第一部分
.files/image163.gif) 一.选择题(每小题5分)
一.选择题(每小题5分)
1.D 2.A 3.C 4.D 5.B 6.D 7.D 8.C 9.A
二.填空题(每小题5分)
10. 12 5.2 11. .files/image165.gif) 12.
19,13 13. 85 14.①③⑷
12.
19,13 13. 85 14.①③⑷
三.解答题
15.(本题9分)
解:如图建系………………………………………1分
则.files/image167.gif) ,则
,则.files/image169.gif) ………… 3分
………… 3分
设交点为P,P为AD中点,则
.files/image171.gif)
16. (本题9分)
解:(1)
分组
0~20
20~40
40~60
60~80
80~100
频数
3
6
12
21
18
频率
0.05
0.10
0.20
0.35
0.3
…………………………………………………………………………3分
(2) 略……………………………………………………………3分
(3)依次记小矩形面积为.files/image173.gif) ,则
,则.files/image175.gif) ,
,.files/image177.gif) ,
,.files/image179.gif) ,
,.files/image181.gif) ………………3分
………………3分
17. (本题12分)
解:(1)设事件.files/image183.gif) 为“方程
为“方程.files/image101.gif) 有实根”.
有实根”.
当.files/image186.gif) ,
,.files/image188.gif) 时,方程
时,方程.files/image101.gif) 有实根的充要条件为
有实根的充要条件为.files/image191.gif) ………………2分.
………………2分.
基本事件共12个:
.files/image193.gif) .其中第一个数表示
.其中第一个数表示.files/image103.gif) 的取值,第二个数表示
的取值,第二个数表示.files/image107.gif) 的取值.……………………………………………… 3分
的取值.……………………………………………… 3分
事件.files/image183.gif) 中包含9个基本事件,即
中包含9个基本事件,即
(0,0),(1,0),(1,1),(2,0),(2,1),(2,2),(3,0),(3,1),(3,2)……………
5分
所以事件.files/image183.gif) 发生的概率为
发生的概率为
.files/image199.gif) .…………………………………………… 6分
.…………………………………………… 6分
(Ⅱ)试验的全部结果所构成的区域为.files/image201.gif) ……………………8分.
……………………8分.
构成事件.files/image183.gif) 的区域为
的区域为.files/image204.gif) ………………………………10分
………………………………10分
所以所求的概率为.files/image206.gif) .………………………………………………………12分
.………………………………………………………12分
第二部分
18.(1).files/image208.gif) ,(2)
,(2).files/image210.gif)
19.(本小题12分)
解:因为.files/image212.gif) ,所以当
,所以当.files/image214.gif) ………………………………………………2分
………………………………………………2分
因为当.files/image216.gif) ,
,
所以,由题意得:当.files/image218.gif) 时,
时,.files/image220.gif) 恒成立……………………4分
恒成立……………………4分
①.files/image222.gif) …………………………………………6分
…………………………………………6分
②设方程.files/image224.gif) 的两根为
的两根为.files/image226.gif) ,则
,则.files/image228.gif) …………………7分
…………………7分
所以.files/image230.gif) ………………………………………………11分
………………………………………………11分
所以,.files/image232.gif) ………………………………………………………………………………12分
………………………………………………………………………………12分
20.(本小题12分)
解:(充分性)已知.files/image234.gif)
假设方程都没有实数根,则.files/image236.gif) …………………………2分
…………………………2分
所以.files/image238.gif) ,与已知
,与已知.files/image234.gif) 矛盾,
矛盾,
所以,假设不成立,即方程至少存在一个有实数根………………………………………6分
所以,.files/image103.gif)
.files/image139.gif) =2(
=2(.files/image107.gif) +
+.files/image141.gif) )是方程
)是方程.files/image143.gif) 与方程
与方程.files/image145.gif) 中至少有一个有实根的充分条件
中至少有一个有实根的充分条件
………………………………………………………………………………………………7分
(必要性)取.files/image240.gif) ,则方程
,则方程.files/image242.gif) 都有实根,
都有实根,
但.files/image244.gif) ,不满足条件
,不满足条件.files/image234.gif) ,所以,
,所以,.files/image103.gif)
.files/image139.gif) =2(
=2(.files/image107.gif) +
+.files/image141.gif) )是方程
)是方程.files/image143.gif) 与方程
与方程.files/image145.gif) 中至少有一个有实根的不必要条件
中至少有一个有实根的不必要条件
即.files/image103.gif)
.files/image139.gif) =2(
=2(.files/image107.gif) +
+.files/image141.gif) )是方程
)是方程.files/image143.gif) 与方程
与方程.files/image145.gif) 中至少有一个有实根的充分不必要条件
中至少有一个有实根的充分不必要条件
………………………………………………………………………………………………………………12分
21.(本小题14分)
解:(1).files/image246.gif) ………………2分
………………2分
若.files/image157.gif) ,则
,则.files/image249.gif) ,所以函数
,所以函数.files/image048.gif) 在区间
在区间.files/image252.gif) 上单调递减,即
上单调递减,即.files/image254.gif)
所以,当.files/image256.gif) 时,
时,.files/image258.gif) ,因为函数为偶函数,所以
,因为函数为偶函数,所以
当.files/image260.gif) 时,
时,.files/image258.gif) ………………………………………………4分
………………………………………………4分
(2)若.files/image262.gif) ,即
,即.files/image264.gif) ,
,.files/image048.gif) 在区间
在区间.files/image252.gif) 上单调递增,即
上单调递增,即.files/image268.gif) ,
,
所以,当.files/image256.gif) 时,
时,.files/image270.gif) …………………………………………7分
…………………………………………7分
因为.files/image272.gif)
若.files/image274.gif) ,即
,即.files/image276.gif) ,当
,当.files/image256.gif) 时,
时,.files/image278.gif) ,
,
所以.files/image280.gif) ………………………………………………………10分
………………………………………………………10分
若若.files/image282.gif) ,即
,即.files/image284.gif) ,当
,当.files/image256.gif) 时,
时,.files/image286.gif) ,
,
所以.files/image288.gif) ………………………………………………………13分
………………………………………………………13分
综上所述,因为函数为偶函数,所以当.files/image260.gif) 时,
时,
.files/image290.gif) ………………………………………………………………14分
………………………………………………………………14分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com