
题目列表(包括答案和解析)
某酒店根据以往的数据统计发现,在预定了客房的客人中,会有20%的人不出现(即不来入住),所以酒店经常采取超额预定的方式,即预订出去的客房数超出可用客房数,由于超额预定酒店会面临的损失包括:若客人未能如约入住而产生一间空房的话,会造成50元的损失;而已经预定房间的客人由于超额预定而不能得到房间时,宾馆会损失100元(将客人安排到其他宾馆的相关费用),现酒店将5间空房预定给了7位客人,设每位预定客房的客人出现与否是相互独立的.
求7人中恰有2人不出现的概率;
求客人来而没有房住的情况发生的概率;
设![]() 为酒店的损失,求
为酒店的损失,求![]() 的分布列及数学期望.
的分布列及数学期望.
(参考数据:![]() ,
,![]() ,
,![]() )
)
设椭圆  :
: (
( )的一个顶点为
)的一个顶点为 ,
, ,
, 分别是椭圆的左、右焦点,离心率
分别是椭圆的左、右焦点,离心率
 ,过椭圆右焦点
,过椭圆右焦点
 的直线
的直线  与椭圆
与椭圆  交于
交于 ,
, 两点.
两点.
(1)求椭圆 的方程;
的方程;
(2)是否存在直线  ,使得
,使得
 ,若存在,求出直线
,若存在,求出直线
 的方程;若不存在,说明理由;
的方程;若不存在,说明理由;
【解析】本试题主要考查了椭圆的方程的求解,以及直线与椭圆的位置关系的运用。(1)中椭圆的顶点为 ,即
,即 又因为
又因为 ,得到
,得到 ,然后求解得到椭圆方程(2)中,对直线分为两种情况讨论,当直线斜率存在时,当直线斜率不存在时,联立方程组,结合
,然后求解得到椭圆方程(2)中,对直线分为两种情况讨论,当直线斜率存在时,当直线斜率不存在时,联立方程组,结合 得到结论。
得到结论。
解:(1)椭圆的顶点为 ,即
,即
 ,解得
,解得 ,
,
 椭圆的标准方程为
椭圆的标准方程为 --------4分
--------4分
(2)由题可知,直线 与椭圆必相交.
与椭圆必相交.
①当直线斜率不存在时,经检验不合题意. --------5分
②当直线斜率存在时,设存在直线 为
为 ,且
,且 ,
, .
.
由 得
得 , ----------7分
, ----------7分
 ,
, ,
,

=
所以 ,
----------10分
,
----------10分
故直线 的方程为
的方程为 或
或
即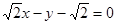 或
或
设函数 .
.
(I)求 的单调区间;
的单调区间;
(II)当0<a<2时,求函数 在区间
在区间 上的最小值.
上的最小值.
【解析】第一问定义域为真数大于零,得到 .
. .
.
令 ,则
,则 ,所以
,所以 或
或 ,得到结论。
,得到结论。
第二问中, (
( ).
).
 .
.
因为0<a<2,所以 ,
, .令
.令 可得
可得 .
.
对参数讨论的得到最值。
所以函数 在
在 上为减函数,在
上为减函数,在 上为增函数.
上为增函数.
(I)定义域为 . ………………………1分
. ………………………1分
 .
.
令 ,则
,则 ,所以
,所以 或
或 . ……………………3分
. ……………………3分
因为定义域为 ,所以
,所以 .
.
令 ,则
,则 ,所以
,所以 .
.
因为定义域为 ,所以
,所以 . ………………………5分
. ………………………5分
所以函数的单调递增区间为 ,
,
单调递减区间为 .
………………………7分
.
………………………7分
(II) (
( ).
).
 .
.
因为0<a<2,所以 ,
, .令
.令 可得
可得 .…………9分
.…………9分
所以函数 在
在 上为减函数,在
上为减函数,在 上为增函数.
上为增函数.
①当 ,即
,即 时,
时,
在区间 上,
上, 在
在 上为减函数,在
上为减函数,在 上为增函数.
上为增函数.
所以 . ………………………10分
. ………………………10分
②当 ,即
,即 时,
时, 在区间
在区间 上为减函数.
上为减函数.
所以 .
.
综上所述,当 时,
时, ;
;
当 时,
时,
已知函数 
 R).
R).
(Ⅰ)若  ,求曲线
,求曲线
 在点
在点  处的的切线方程;
处的的切线方程;
(Ⅱ)若  对任意
对任意 
 恒成立,求实数a的取值范围.
恒成立,求实数a的取值范围.
【解析】本试题主要考查了导数在研究函数中的运用。
第一问中,利用当 时,
时, .
.
 因为切点为(
因为切点为( ),
则
),
则 ,
,
所以在点( )处的曲线的切线方程为:
)处的曲线的切线方程为:
第二问中,由题意得, 即
即 即可。
即可。
Ⅰ)当 时,
时, .
.
 ,
,
因为切点为( ),
则
),
则 ,
,
所以在点( )处的曲线的切线方程为:
)处的曲线的切线方程为: . ……5分
. ……5分
(Ⅱ)解法一:由题意得, 即
即 . ……9分
. ……9分
(注:凡代入特殊值缩小范围的均给4分)
 ,
,
因为 ,所以
,所以 恒成立,
恒成立,
故 在
在 上单调递增,
……12分
上单调递增,
……12分
要使 恒成立,则
恒成立,则 ,解得
,解得 .……15分
.……15分
解法二: ……7分
……7分
(1)当 时,
时, 在
在 上恒成立,
上恒成立,
故 在
在 上单调递增,
上单调递增,
 即
即 .
……10分
.
……10分
(2)当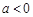 时,令
时,令 ,对称轴
,对称轴 ,
,
则 在
在 上单调递增,又
上单调递增,又
① 当 ,即
,即 时,
时, 在
在 上恒成立,
上恒成立,
所以 在
在 单调递增,
单调递增,
 即
即 ,不合题意,舍去
,不合题意,舍去
②当 时,
时, ,
不合题意,舍去 14分
,
不合题意,舍去 14分
综上所述:
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com