题目列表(包括答案和解析)
如图所示，x轴正方向水平向右，y轴正方向竖直向上。在xOy
平面内有与y轴平行的匀强电场，在半径为R的圆内还有与xOy平面垂直的匀强磁场。在圆的左边放置一带电微粒发射装置，它沿x轴正方向发射出一束具有相同质量m、电荷量q（q＞0)和初速度v的带电微粒。发射时，这束带电微粒分布在0＜y＜2R的区间内。已知重力加速度大小为g。
（1）从A点射出的带电微粒平行于x轴从C点进入有磁场区域，并从坐标原点O沿y轴负方向离开，求电场强度和磁感应强度的大小与方向。
（2）请指出这束带电微粒与x轴相交的区域，并说明理由。
（3）若这束带电微粒初速度变为2v，那么它们与x轴相交的区域又在哪里？并说明理由。
带电粒子的质量为m，电量为q，以初速度v沿y轴正方向从原点O射入一半径为r的圆形磁场区域后，又从磁场射出．圆形磁场垂直于xOy平面，磁场边界过坐标原点O，磁感应强度为B，带电粒子的重力不计，它在磁场中做匀速圆周运动，轨迹圆半径R＞r．
(1)改变磁场区域的位置，可以改变带电粒子穿越磁场时的速度偏转角，为使偏转角有最大值，该磁场区域的圆心应在什么位置，最大偏转角多大?
(2)为使带电粒子从圆形磁场区域中射出后能通过Ox轴上某点，该磁场区域半径应满足怎样的条件?
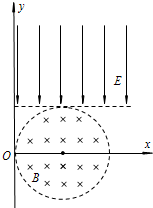利用电场、磁场可以控制带电粒子的运动．如图所示，在平面直角坐标系xOy中，有一个半径为r的圆形区域，其圆心坐标为 （r，0）．在这个区域内存在磁感应强度大小为B、方向垂直于xOy平面向里的匀强磁场．在直线y=r的上方足够大的区域内，存在沿y轴负方向的匀强电场，电场强度的大小为E．一质子从O点沿x轴正方向射入磁场，在磁场中做半径为r的匀速圆周运动．已知质子的质量为m，电荷量为q，不计质子的重力．求：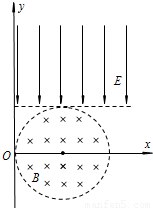
第I卷 选择题
1.A 2.C 3.B 4.C 5.B 6. C 7.B 8.A 9. D 10. C 11. A 12.C 13.B
14. C 15 .A 16.B 17.ACD 18. BC 19.B 20. BD 21. AD
第II卷 非选择题
22 I 0.590 2.642
每空2分，共4分。
Ⅱ（1）E；C
（2）甲
（3）连接实物图
（4）①变大 ②10Ω
（1）每空1分（2）3分（3）4分（4）每空2分。
23．
（1）由小物块上滑过程的速度―时间图线，可知：
（3分）
m/s2
（1分）
小物块冲上斜面过程中加速度的大小为
（2）小物块受重力、支持力、摩擦力，沿斜面建立直角坐标系，
（2分）
（2分）
（2分）
代入数据解得 
（2分）
（3）设物块冲上斜面所能达到的最高点距斜面底端距离为s，
向上运动阶段 
（3分）
（1分）
24．解：小车在半径为R的圆周上作圆周运动，处于圆周轨道的最高点时，小车和人所受重力之和提供向心力，设小车滑行到D点时的速度为u，根据牛顿第二定律
（4分）
得u=
m
设人和小车以共同速度v ，从水平面运动到D的过程中机械能守恒，根据机械能守恒定律得
（4分）
v=15m/s （2分）
在人接触小车，并使小车和人一起前进的过程中，无水平方向外力作用，故水平方向上动量守恒，得
(4分)
v0=20m/s （3分）
25．（1）质子射入磁场后做匀速圆周运动，有
evB=mv2/r （3分）
可得v=eBr/m （1分）
（2）质子沿x轴正向射入磁场后经1/4圆弧后以速度v垂直于电场方向进入电场，周期为
（2分）
在磁场中运动的时间
t1=T/4=πm/2eB （1分）
进入电场后做抛物线运动，沿电场方向运动r后到达y轴，因此有
（1分）
t2=
（1分）
所求时间为t=
t1+ t2=
（1分）
（3）质子在磁场中转过120°角后从P点垂直电场线进入电场，如图所示。
P点距y轴的距离
x1=r+rsin30°=1.5r 
（2分）
因此可得质子从进入电场至到达y轴所需时间为
=
（2分）
质子在电场中沿y轴方向做匀速直线运动，因此有
（2分）
质子到达y轴的位置坐标为
即（0，r+
） (2分)
图 （2分）
26．（10分）（1）N2 （2分）
 |
（2） （2分，如写出CO正确的电子式也给分）
（3）离子键、非极性键。（2分，第二空答共价键也给分） ②④ （2分，答案全正确给分）
（4）CS2+2H2O
CO2+2H2S（2分）
27．（18分）（1）Al+4OH-?3e- = AlO2-+2H2O(2分)
（2）10-2?10-12 mol/L， 或c(OH-)?c(H+) (2分) < (2分)
（3）否(1分)；因为A的氯化物熔沸点低，据此判断它的晶体为分子晶体，在熔融态时不电离，不能被电解(2分)。
 |
（4）4NH3+5O2 4NO+6H2O （2分，条件错误扣1分）
|
（4）
（5）
（2分）
29．（17分）（1）①
（7分，前五个空每空一分，最后一空两结论各一分。本题其它合理答案均给分）