设a_n=2ⁿ，b_n=n，（n=1，2，3，。。。），A_n、B_n分别为数列{a_n}、{b_n}的前n项和。记c_n=a_nB_n+b_nA_n―a_nb_n，则数列{c_n}的前10项和为

A．2¹⁰+53                        B.2 ¹¹ +53

C.110×（2 ⁹－1）                D.110×（2 ¹⁰－1）

．设a_n=2ⁿ，b_n=n，（n=1，2，3，。。。），A_n、B_n分别为数列{a_n}、{b_n}的前n项和。记c_n=a_nB_n+b_nA_n―a_nb_n，则数列{c_n}的前10项和为

A．2¹⁰+53                        B.2 ¹¹ +53

C.110×（2 ⁹－1）                D.110×（2 ¹⁰－1）

在古希腊，毕达哥拉斯学派把1，3，6，10，15，21，28，…，这些数叫做三角形数，其通项为

n(n+1)

2

，前n项和为sn=

n(n+1)(n+2)

6

，如下图所示，有一列三角形数表，其位于三角形的三边及平行于某边的任一直线上的数（当数的个数不少于3时）都分别依次成等差数列，依次记各三角形数表中的所有数之和为a_n，则a1=

0+2+6

4

=

2(1+3)

4

=2，a2=

0+3+9+18

9

=

3(1+3+6)

9

=

10

3

．
（1）求a₃，a₄，并写出a_n的表达式；
（2）令b_n=

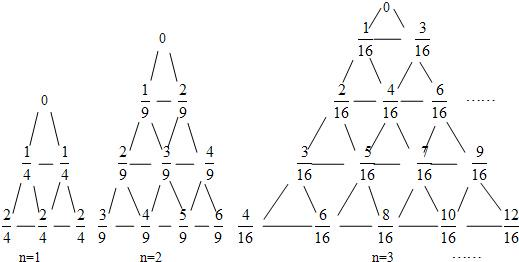
an

an+1

+

an+1

an

，证明2n＜b₁+b₂+b₃+…+b_n＜2n+2（n∈N^*）．

（本小题满分12分）在第9届校园文化艺术节棋类比赛项目报名过程中，我校高二(2)班共有16名男生和14名女生预报名参加，调查发现，男、女选手中分别有10人和6人会围棋.

（I）根据以上数据完成以下22列联表：

	会围棋	不会围棋	总计
男
女
总计			30

并回答能否在犯错的概率不超过0．10的前提下认为性别与会围棋有关？

参考公式：其中n=a+b+c+d

参考数据：

	0.40	0.25	0.10	0.010
	0.708	1.323	2.706	6.635

（Ⅱ）若从会围棋的选手中随机抽取3人成立该班围棋代表队，则该代表队中既有男又

有女的概率是多少？

（Ⅲ）若从14名女棋手中随机抽取2人参加棋类比赛，记会围棋的人数为，求的期望.