在空间中，给出下列4个命题(其中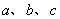表示直线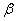，表示平面)，则正确命题的序号是                                                 [答](    )

(1)三个点确定一个平面；

(2)若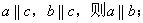

(3)在空间中，若角的两边分别平行，则；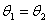

(4)若．

　　　A．(1)、(2)、(4)．　B．(2)．  C．(2)、(3)．  D．(2)、(3)、(4)．

 

 

x －2 0 4 f (x) 1 －1 1

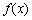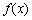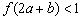已知函数的定义域为[－2，+∞)，部分对应值如下表,为的导函数，函数的图象如右图所示，若两正数a，b满足，则的取值范围是　 　．

 

 

4. m>2或m<-2 解析：因为f(x)=在（-1，1）内有零点，所以f(-1)f(1)<0,即（2+m）(2-m)<0，则m>2或m<-2

随机变量的所有等可能取值为1,2…,n，若，则（    ）

A． n=3　      　B．n=4　　        C． n=5　　      D．不能确定

5.m=-3,n=2 解析：因为的两零点分别是1与2，所以，即，解得

6．解析：因为只有一个零点，所以方程只有一个根，因此，所以

5．A解析：因为函数有0，1，2三个零点，可设函数为f(x)=ax(x-1)(x-2)=ax3-3ax2+2ax

因此b=-3a,又因为当x>2时f(x)>0所以a>0,因此b<0

若由一个2*2列联表中的数据计算得k=4.013,那么有          把握认为两个变量有关系.

已知函数．

（Ⅰ）求函数的单调区间；

（Ⅱ）设，若对任意，，不等式 恒成立，求实数的取值范围．

【解析】第一问利用的定义域是     

由x>0及 得1<x<3；由x>0及得0<x<1或x>3，

故函数的单调递增区间是（1,3）；单调递减区间是

第二问中，若对任意不等式恒成立，问题等价于只需研究最值即可。

解： （I）的定义域是     ．．．．．．1分

              ．．．．．．．．．．．．． 2分

由x>0及 得1<x<3；由x>0及得0<x<1或x>3，

故函数的单调递增区间是（1,3）；单调递减区间是     ．．．．．．．．4分

（II）若对任意不等式恒成立，

问题等价于，                   ．．．．．．．．．5分

由（I）可知，在上，x=1是函数极小值点，这个极小值是唯一的极值点，

故也是最小值点，所以；            ．．．．．．．．．．．．6分

当b<1时，；

当时，；

当b>2时，；             ．．．．．．．．．．．．8分

问题等价于 ．．．．．．．．11分

解得b<1 或 或    即，所以实数b的取值范围是