已知是等差数列，其前n项和为S_n，是等比数列，且，.

（Ⅰ）求数列与的通项公式；

（Ⅱ）记，，证明（）.

【解析】（1）设等差数列的公差为d，等比数列的公比为q.

由，得，，.

由条件，得方程组，解得

所以，，.

（2）证明：（方法一）

由（1）得

     ①

   ②

由②-①得

而

故，

（方法二：数学归纳法）

①  当n=1时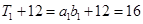，，，故等式成立.

②  假设当n=k时等式成立，即，则当n=k+1时，有：

   

   

即，因此n=k+1时等式也成立

由①和②，可知对任意，成立.

 

选择题．

(1)由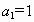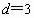，确定的等差数列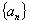，当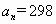时，序号n等于

[　　］

(A)99．

(B)100．

(C)96．

(D)101．

(2)一个蜂巢里有1只蜜蜂．第1天，它飞出去找回了5个伙伴；第2天，6只蜜蜂飞出去，各自找回了5个伙伴……如果这个找伙伴的过程继续下去，第6天所有的蜜蜂都归巢后，蜂巢中一共有(　　)只蜜蜂．

[　　]

(A)55986．

(B)46656．

(C)216．

(D)36．

(3)预测人口的变化趋势有多种方法，“直接推算法”使用的公式是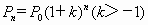，其中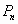为预测期人口数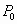，为初期人口数，k为预测期内年增长率，n为预测期间隔年数．如果在某一时期有－1＜k＜0，那么在这期间人口数

[　　]

(A)呈上升趋势．

(B)呈下降趋势．

(C)摆动变化．

(D)不变．

(4)《莱因德纸草书》(Rhind Papyrus)是世界上最古老的数学著作之一．书中有一道这样的题目：把100个面包分给5个人，使每人所得成等差数列，且使较大的三份之和的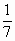是较小的两份之和，问最小1份为

[　　]

(A)．

(B)．

(C)．

(D)．

已知数列是各项均不为0的等差数列，公差为d，为其前n项和，且满足,．数列满足,，为数列的前n项和．

（1）求数列的通项公式和数列的前n项和；

（2）若对任意的，不等式恒成立，求实数的取值范围；

（3）是否存在正整数，使得成等比数列？若存在，求出所有的值；若不存在，请说明理由．

【解析】第一问利用在中，令n=1，n=2，

得   即      

解得，， [

又时，满足，

，

第二问，①当n为偶数时，要使不等式恒成立，即需不等式恒成立．   

 ，等号在n=2时取得．

此时 需满足．  

②当n为奇数时，要使不等式恒成立，即需不等式恒成立．     

 是随n的增大而增大， n=1时取得最小值-6．

此时 需满足．

第三问，

     若成等比数列，则，

即．

由，可得，即，

        ．

（1）（法一）在中，令n=1，n=2，

得   即      

解得，， [

又时，满足，

，

．

（2）①当n为偶数时，要使不等式恒成立，即需不等式恒成立．   

 ，等号在n=2时取得．

此时 需满足．  

②当n为奇数时，要使不等式恒成立，即需不等式恒成立．     

 是随n的增大而增大， n=1时取得最小值-6．

此时 需满足．

综合①、②可得的取值范围是．

（3），

     若成等比数列，则，

即．

由，可得，即，

．

又，且m>1，所以m=2，此时n=12．

因此，当且仅当m=2， n=12时，数列中的成等比数列