
题目列表(包括答案和解析)
(本小题满分12分)数列![]() 的通项是关于
的通项是关于![]() 的不等式
的不等式![]() 的解集中整数的个数,
的解集中整数的个数,![]() (1)求数列
(1)求数列![]() 的通项公式; (2)是否存在实数
的通项公式; (2)是否存在实数![]() 使不等式
使不等式![]() 对一切大于1的自然数
对一切大于1的自然数![]() 恒成立,若存在试确定
恒成立,若存在试确定![]() 的取值范围,否则说明原因.
的取值范围,否则说明原因.
已知函数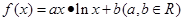 ,在点
,在点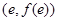 处的切线方程是
处的切线方程是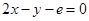 (e为自然对数的底)。
(e为自然对数的底)。
(1)求实数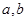 的值及
的值及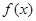 的解析式;
的解析式;
(2)若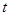 是正数,设
是正数,设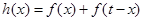 ,求
,求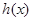 的最小值;
的最小值;
(3)若关于x的不等式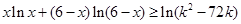 对一切
对一切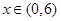 恒成立,求实数
恒成立,求实数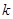 的取值范围.
的取值范围.
已知函数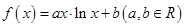 ,在点
,在点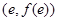 处的切线方程是
处的切线方程是 (e为自然对数的底)。
(e为自然对数的底)。
(1)求实数 的值及
的值及 的解析式;
的解析式;
(2)若 是正数,设
是正数,设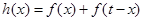 ,求
,求 的最小值;
的最小值;
(3)若关于x的不等式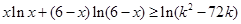 对一切
对一切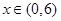 恒成立,求实数
恒成立,求实数 的取值范围。
的取值范围。
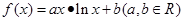 ,在点
,在点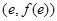 处的切线方程是
处的切线方程是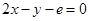 (e为自然对数的底)。
(e为自然对数的底)。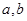 的值及
的值及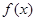 的解析式;
的解析式;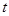 是正数,设
是正数,设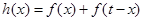 ,求
,求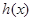 的最小值;
的最小值;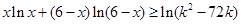 对一切
对一切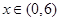 恒成立,求实数
恒成立,求实数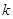 的取值范围.
的取值范围.已知f(x)是定义在R上的不恒为零的函数,且对于任意的a、b∈R都满足f(a·b)=af(b)+bf(a).
(1)求f(0),f(1)的值;
(2)判断f(x)的奇偶性,并证明你的结论;
(3)若 Sn表示数列{bn}的前n项和.试问:是否存在关于n的整式g(n),使得S1+S2+S3+…+Sn-1=(Sn-1)·g(n)对于一切不小于2的自然数n恒成立?若存在,写出g(n)的解析式,并加以证明;若不存在,试说明理由.
Sn表示数列{bn}的前n项和.试问:是否存在关于n的整式g(n),使得S1+S2+S3+…+Sn-1=(Sn-1)·g(n)对于一切不小于2的自然数n恒成立?若存在,写出g(n)的解析式,并加以证明;若不存在,试说明理由.
一、选择题(本大题共8小题,每小题5分,共40分)
1.B 2. D 3.B 4.B 5.A 6.A 7.C 8. A.
二、填空题(本大题共6小题,每小题5分,共30分)
9.2009.4.10.files/image232.gif) 10. 4
11.
10. 4
11. 2009.4.10.files/image234.gif) (2分),
(2分),2009.4.10.files/image236.gif) (3分)
(3分)
12.2009.4.10.files/image238.gif) 13.
13. 2009.4.10.files/image240.gif) 14.
14.2009.4.10.files/image242.gif) 15.
15. 2009.4.10.files/image244.gif)
三、解答题(本大题共6小题,共80分)
16.(本题满分10分)
解:(1)由向量2009.4.10.files/image246.gif) 共线有:
共线有: 2009.4.10.files/image248.gif)
即2009.4.10.files/image250.gif) ,
4分
,
4分
又2009.4.10.files/image252.gif) ,所以
,所以2009.4.10.files/image254.gif) ,
,
则2009.4.10.files/image256.gif) =
=2009.4.10.files/image258.gif) ,即
,即2009.4.10.files/image260.gif) 6分
6分
(2)由余弦定理得2009.4.10.files/image262.gif)
则2009.4.10.files/image264.gif) ,
,
所以2009.4.10.files/image266.gif) 当且仅当
当且仅当2009.4.10.files/image268.gif) 时等号成立 10分
时等号成立 10分
所以2009.4.10.files/image270.gif) .
12分
.
12分
17.(本小题满分12分)
解:(1)由已知条件得
2009.4.10.files/image272.gif) 2分
2分
即2009.4.10.files/image274.gif) ,则
,则2009.4.10.files/image276.gif) 6分
6分
答:2009.4.10.files/image080.gif) 的值为
的值为2009.4.10.files/image279.gif) .
.
(2)解:2009.4.10.files/image175.gif) 可能的取值为0,1,2,3 5分
可能的取值为0,1,2,3 5分
2009.4.10.files/image282.gif) 6分
6分
2009.4.10.files/image284.gif)
2009.4.10.files/image286.gif) 7分
7分
2009.4.10.files/image288.gif) 8分
8分
2009.4.10.files/image175.gif) 的分布列为:
的分布列为:
2009.4.10.files/image175.gif)
0
1
2
3
2009.4.10.files/image292.gif)
2009.4.10.files/image294.gif)
2009.4.10.files/image173.gif)
2009.4.10.files/image297.gif)
2009.4.10.files/image299.gif)
10分
所以2009.4.10.files/image301.gif)
2009.4.10.files/image303.gif) 12分
12分
答:数学期望为2009.4.10.files/image305.gif) .
.
18.(本小题满分14分)
解:(1) 在△PAC中,∵PA=3,AC=4,PC=5,
2009.4.10.files/image307.jpg) ∴
∴2009.4.10.files/image309.gif) ,∴
,∴2009.4.10.files/image311.gif) ;……1分
;……1分
又AB=4,PB=5,∴在△PAB中,
同理可得 2009.4.10.files/image313.gif) …………………………2分
…………………………2分
∵2009.4.10.files/image315.gif) ,∴
,∴2009.4.10.files/image317.gif) ……3分
……3分
∵2009.4.10.files/image319.gif) 平面ABC,∴PA⊥BC. …………4分
平面ABC,∴PA⊥BC. …………4分
(2) 如图所示取PC的中点G,…………………5分
连结AG,BG,∵PF:FC=3:1,∴F为GC的中点
又D、E分别为BC、AC的中点,
∴AG∥EF,BG∥FD,又AG∩GB=G,EF∩FD=F,……………7分
∴面ABG∥面DEF.
即PC上的中点G为所求的点. …………… 9分
(3)由(2)知G这PC的中点,连结GE,∴GE⊥平面ABC,过E作EH⊥AB于H,连结GH,则GH⊥AB,∴∠EHG为二面角G-AB-C的平面角. …………… 11分
∵2009.4.10.files/image321.gif) 又
又2009.4.10.files/image323.gif)
∴2009.4.10.files/image325.gif) 又
又2009.4.10.files/image327.gif) …………… 13分
…………… 13分
∴2009.4.10.files/image329.gif)
∴二面角G-AB-C的平面角的正切值为2009.4.10.files/image331.gif) .
…………… 14分
.
…………… 14分
19.(本小题满分14分)
① 当2009.4.10.files/image379.gif) 时,
时,2009.4.10.files/image040.gif) 在
在2009.4.10.files/image350.gif) 上单调递减,
上单调递减,2009.4.10.files/image383.gif) ,
,2009.4.10.files/image385.gif) (舍去),所以,此时
(舍去),所以,此时2009.4.10.files/image040.gif) 无最小值. ……10分
无最小值. ……10分
③ 当2009.4.10.files/image398.gif) 时,
时,2009.4.10.files/image040.gif) 在
在2009.4.10.files/image350.gif) 上单调递减,
上单调递减,2009.4.10.files/image383.gif) ,
,2009.4.10.files/image385.gif) (舍去),所以,此时
(舍去),所以,此时2009.4.10.files/image040.gif) 无最小值.综上,存在实数
无最小值.综上,存在实数2009.4.10.files/image396.gif) ,使得当
,使得当2009.4.10.files/image373.gif) 时
时2009.4.10.files/image040.gif) 有最小值3.……14分
有最小值3.……14分
20.解(1)∵2009.4.10.files/image404.gif) 过(0,0)
过(0,0)
则2009.4.10.files/image406.gif)
|