
题目列表(包括答案和解析)
(本小题满分12分)
如图,△ABC内接于圆O,AB是圆O的直径,四边形DCBE为平行四边形,DC⊥平面ABC ,AB=2,已知AE与平面ABC所成的角为θ,且tanθ=。
(Ⅰ)证明:平面ACD⊥平面ADE;
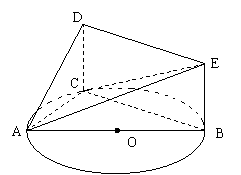 (Ⅱ)记AC=x,V(x)表示三棱锥A-CBE的体积,求V(x)的表达式;
(Ⅱ)记AC=x,V(x)表示三棱锥A-CBE的体积,求V(x)的表达式;
(Ⅲ)当V(x)取得最大值时,求二面角D-AB-C的大小。
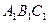 平行于三棱锥
平行于三棱锥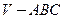 的底面,等边三角形
的底面,等边三角形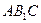 所在平面与面
所在平面与面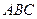 垂直,且
垂直,且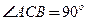 ,设
,设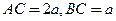 。
。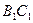 为异面直线
为异面直线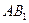 与
与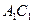 的公垂线;
的公垂线;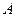 与平面
与平面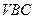 的距离;
的距离;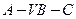 的大小。
的大小。()(本小题满分12分)如图,已知平面![]() 平行于三棱锥
平行于三棱锥![]() 的底面,等边三角形
的底面,等边三角形![]() 所在平面与面
所在平面与面![]() 垂直,且
垂直,且![]() ,设
,设![]() 。
。
(Ⅰ)证明:![]() 为异面直线
为异面直线![]() 与
与![]() 的公垂线;
的公垂线;
(Ⅱ)求点![]() 与平面
与平面![]() 的距离;
的距离;
(Ⅲ)求二面角![]() 的大小。
的大小。
(本小题满分12分)
医生的专业能力参数K可有效衡量医生的综合能力,K越大,综合能力越强,并规定:能力参数K不少于30称为合格,不少于50称为优秀,某市卫生管理部门随机抽取300名医生进行专业能力参数考核,得到如图所示的能力参数K的频率颁布直方图:
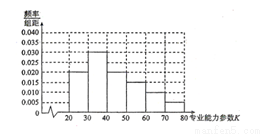
(1)求这个样本的合格率、优秀率,并估计能力参数K的平均值;
(2)现用分层抽样的方法从中抽出一个样本容量为20的样本,再从这20名医生中随机选出2名。
①求这2名医生的能力参数K为同一组的概率;
②设这2名医生中能力参数K为优秀的的人数为X,求随机变量X的分布列和期望。
(本小题满分12分)(注意:在试题卷上作答无效)

如图,在四棱锥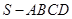 中,底面
中,底面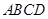 为平行四边形,侧面
为平行四边形,侧面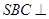 底面
底面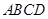 .已知
.已知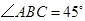 ,
,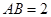 ,
,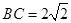 ,
,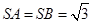 .
.
(Ⅰ)证明 ;
;
(Ⅱ)求直线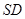 与平面
与平面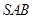 所成角的大小.
所成角的大小.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com