练习册

  • 练习册
  • 试题
    当且仅当.即时.等号成立.故四边形MRNQ的面积的最小值为72．12分 【查看更多】

     

    题目列表(包括答案和解析)

    一段长为32米的篱笆围成一个一边靠墙的矩形菜园，墙长18米，问这个矩形的长、宽各为多少时，菜园的面积最大，最大面积是多少？

    【解析】解：令矩形与墙垂直的两边为宽并设矩形宽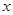为，则长为

    所以矩形的面积   （）     （4分=128    （8分）

    当且仅当时，即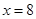时等号成立，此时有最大值128

    所以当矩形的长为=16，宽为8时，

    菜园面积最大，最大面积为128 （13分）答：当矩形的长为16米，宽为8米时。菜园面积最大，最大面积为128平方米（注：也可用二次函数模型解答）

     

    查看答案和解析>>

    （2008•奉贤区模拟）我们将具有下列性质的所有函数组成集合M：函数y=f（x）（x∈D），对任意x，y，
    x+y
    2
    ∈D    均满足f(
    x+y
    2
    )≥
    1
    2
    [f(x)+f(y)]    ，当且仅当x=y时等号成立．
    （1）若定义在（0，+∞）上的函数f（x）∈M，试比较f（3）+f（5）与2f（4）大小．
    （2）给定两个函数：f1(x)=
    1
    x
    (x＞0)    ，f2（x）=logax（a＞1，x＞0）．证明：f1（x）∉M，f2（x）∈M．
    （3）试利用（2）的结论解决下列问题：若实数m、n满足2m+2n=1，求m+n的最大值．

    查看答案和解析>>

    （2008•奉贤区一模）我们将具有下列性质的所有函数组成集合M：函数y=f（x）（x∈D），对任意x，y，
    x+y
    2
    ∈D    均满足f(
    x+y
    2
    )≥
    1
    2
    [f(x)+f(y)]    ，当且仅当x=y时等号成立．
    （1）若定义在（0，+∞）上的函数f（x）∈M，试比较f（3）+f（5）与2f（4）大小．
    （2）设函数g（x）=-x2，求证：g（x）∈M．
    （3）已知函数f（x）=log2x∈M．试利用此结论解决下列问题：若实数m、n满足2m+2n=1，求m+n的最大值．

    查看答案和解析>>

    已知a，b都是正数，求证：
    2ab
    a+b
    ≤
    a+b
    2
    ≤
    a2+b2
    2
    ，当且仅当a=b时等号成立．

    查看答案和解析>>

    （1）已知a，b，x，y是正实数，求证：
    a2
    x
    +
    b2
    y
    ≥
    (a+b)2
    x+y
    ，当且仅当
    a
    x
    =
    b
    y
    时等号成立；
    （2）求函数f(x)=
    1
    3-tan2x
    +
    9
    8+sec2x
    的最小值，并指出取最小值时x的值．

    查看答案和解析>>


    同步练习册答案