
题目列表(包括答案和解析)
已知函数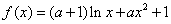 .
.
(Ⅰ)讨论函数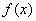 的单调性;
的单调性;
(Ⅱ)设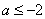 ,证明:对任意
,证明:对任意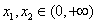 ,
,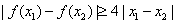 .
.
 1.选修4-1:几何证明选讲
1.选修4-1:几何证明选讲
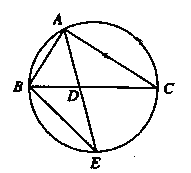
如图, 的角平分线
的角平分线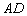 的延长线交它的外接圆于点
的延长线交它的外接圆于点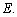
(Ⅰ)证明: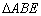 ∽△
∽△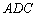 ;
;
(Ⅱ)若 的面积
的面积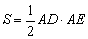 ,求
,求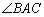 的大小.
的大小.
证明:(Ⅰ)由已知条件,可得∠BAE=∠CAD.
因为∠AEB与∠ACB是同弧上的圆周角,所以∠AEB=∠ACD.
故△ABE∽△ADC.
(Ⅱ)因为△ABE∽△ADC,所以 ,即AB·AC=AD·AE.
,即AB·AC=AD·AE.
又S= AB·ACsin∠BAC,且S=
AB·ACsin∠BAC,且S= AD·AE,故AB·ACsin∠BAC=AD·AE.
AD·AE,故AB·ACsin∠BAC=AD·AE.
则sin∠BAC=1,又∠BAC为三角形内角,所以∠BAC=90°.
如图,三棱锥 中,侧面
中,侧面 底面
底面 ,
,  ,且
,且 ,
, .(Ⅰ)求证:
.(Ⅰ)求证: 平面
平面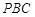 ;
;
(Ⅱ)若 为侧棱PB的中点,求直线AE与底面
为侧棱PB的中点,求直线AE与底面 所成角的正弦值.
所成角的正弦值.

【解析】第一问中,利用由 知,
知,  ,
,
又AP=PC=2,所以AC=2 ,
,
又AB=4, BC=2 ,,所以
,,所以 ,所以
,所以 ,即
,即 ,
,
又平面 平面ABC,平面
平面ABC,平面 平面ABC=AC,
平面ABC=AC,  平面ABC,
平面ABC,
 平面ACP,所以
平面ACP,所以 第二问中结合取AC中点O,连接PO、OB,并取OB中点H,连接AH、EH,因为PA=PC,所以PO⊥AC,同(Ⅰ)易证
第二问中结合取AC中点O,连接PO、OB,并取OB中点H,连接AH、EH,因为PA=PC,所以PO⊥AC,同(Ⅰ)易证 平面ABC,又EH//PO,所以EH平面
平面ABC,又EH//PO,所以EH平面 ABC ,
ABC ,
则 为直线AE与底面ABC 所成角,
为直线AE与底面ABC 所成角,

解
(Ⅰ) 证明:由用由 知,
知,  ,
,
又AP=PC=2,所以AC=2 ,
,
又AB=4, BC=2 ,,所以
,,所以 ,所以
,所以 ,即
,即 ,
,
又平面 平面ABC,平面
平面ABC,平面 平面ABC=AC,
平面ABC=AC,  平面ABC,
平面ABC,
 平面ACP,所以
平面ACP,所以
………………………………………………6分
(Ⅱ)如图, 取AC中点O,连接PO、OB,并取OB中点H,连接AH、EH,
因为PA=PC,所以PO⊥AC,同(Ⅰ)易证 平面ABC,
平面ABC,
又EH//PO,所以EH平面 ABC ,
ABC ,
则 为直线AE与底面ABC 所成角,
为直线AE与底面ABC 所成角,
且 ………………………………………10分
………………………………………10分
又PO=1/2AC= ,也所以有EH=1/2PO=
,也所以有EH=1/2PO= ,
,
由(Ⅰ)已证 平面PBC,所以
平面PBC,所以 ,即
,即 ,
,
故 ,
,
于是
所以直线AE与底面ABC 所成角的正弦值为

如图所示的长方体 中,底面
中,底面 是边长为
是边长为 的正方形,
的正方形, 为
为 与
与 的交点,
的交点, ,
, 是线段
是线段 的中点.
的中点.
(Ⅰ)求证: 平面
平面 ;
;
(Ⅱ)求证: 平面
平面 ;
;
(Ⅲ)求二面角 的大小.
的大小.
【解析】本试题主要考查了线面平行的判定定理和线面垂直的判定定理,以及二面角的求解的运用。中利用 ,又
,又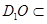 平面
平面 ,
, 平面
平面 ,∴
,∴ 平面
平面 由
由 ,
, ,又
,又 ,∴
,∴ 平面
平面 .
可得证明
.
可得证明
(3)因为∴ 为面
为面 的法向量.∵
的法向量.∵ ,
, ,
,
∴ 为平面
为平面 的法向量.∴利用法向量的夹角公式,
的法向量.∴利用法向量的夹角公式, ,
,
∴ 与
与 的夹角为
的夹角为 ,即二面角
,即二面角 的大小为
的大小为 .
.
方法一:解:(Ⅰ)建立如图所示的空间直角坐标系.连接 ,则点
,则点 、
、 ,
,

∴ ,又点
,又点 ,
, ,∴
,∴
∴ ,且
,且 与
与 不共线,∴
不共线,∴ .
.
又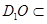 平面
平面 ,
, 平面
平面 ,∴
,∴ 平面
平面 .…………………4分
.…………………4分
(Ⅱ)∵ ,
,
∴ ,
, ,即
,即 ,
, ,
,
又 ,∴
,∴ 平面
平面 . ………8分
. ………8分
(Ⅲ)∵ ,
, ,∴
,∴ 平面
平面 ,
,
∴ 为面
为面 的法向量.∵
的法向量.∵ ,
, ,
,
∴ 为平面
为平面 的法向量.∴
的法向量.∴ ,
,
∴ 与
与 的夹角为
的夹角为 ,即二面角
,即二面角 的大小为
的大小为
在四棱锥 中,
中, 平面
平面 ,底面
,底面 为矩形,
为矩形, .
.
(Ⅰ)当 时,求证:
时,求证: ;
;
(Ⅱ)若 边上有且只有一个点
边上有且只有一个点 ,使得
,使得 ,求此时二面角
,求此时二面角 的余弦值.
的余弦值.

【解析】第一位女利用线面垂直的判定定理和性质定理得到。当a=1时,底面ABCD为正方形,

又因为 ,
, ………………2分
………………2分
又 ,得证。
,得证。
第二问,建立空间直角坐标系,则B(1,0,1)D(0,a,0)C(1,a,0)P(0,0,1)……4分
设BQ=m,则Q(1,m,0)(0《m《a》
要使 ,只要
,只要
所以 ,即
,即 ………6分
………6分
由此可知 时,存在点Q使得
时,存在点Q使得
当且仅当m=a-m,即m=a/2时,BC边上有且只有一个点Q,使得
由此知道a=2, 设平面POQ的法向量为
 ,所以
,所以 平面PAD的法向量
平面PAD的法向量
则 的大小与二面角A-PD-Q的大小相等所以
的大小与二面角A-PD-Q的大小相等所以
因此二面角A-PD-Q的余弦值为
解:(Ⅰ)当 时,底面ABCD为正方形,
时,底面ABCD为正方形,

又因为 ,
, 又
又
 ………………3分
………………3分
(Ⅱ) 因为AB,AD,AP两两垂直,分别以它们所在直线为X轴、Y轴、Z轴建立坐标系,如图所示,

则B(1,0,1)D(0,a,0)C(1,a,0)P(0,0,1)…………4分
设BQ=m,则Q(1,m,0)(0《m《a》要使 ,只要
,只要
所以 ,即
,即 ………6分
………6分
由此可知 时,存在点Q使得
时,存在点Q使得
当且仅当m=a-m,即m=a/2时,BC边上有且只有一个点Q,使得 由此知道a=2,
由此知道a=2,
设平面POQ的法向量为
 ,所以
,所以 平面PAD的法向量
平面PAD的法向量
则 的大小与二面角A-PD-Q的大小相等所以
的大小与二面角A-PD-Q的大小相等所以
因此二面角A-PD-Q的余弦值为
已知中心在坐标原点,焦点在 轴上的椭圆C;其长轴长等于4,离心率为
轴上的椭圆C;其长轴长等于4,离心率为 .
.
(Ⅰ)求椭圆C的标准方程;
(Ⅱ)若点 (0,1), 问是否存在直线
(0,1), 问是否存在直线 与椭圆
与椭圆 交于
交于 两点,且
两点,且 ?若存在,求出
?若存在,求出 的取值范围,若不存在,请说明理由.
的取值范围,若不存在,请说明理由.
【解析】本试题主要考查了椭圆的方程的求解,直线与椭圆的位置关系的运用。
第一问中,可设椭圆的标准方程为
则由长轴长等于4,即2a=4,所以a=2.又 ,所以
,所以 ,
,
又由于
所求椭圆C的标准方程为
第二问中,
假设存在这样的直线 ,设
,设 ,MN的中点为
,MN的中点为
因为|ME|=|NE|所以MN EF所以
EF所以
(i)其中若 时,则K=0,显然直线
时,则K=0,显然直线 符合题意;
符合题意;
(ii)下面仅考虑 情形:
情形:
由 ,得,
,得,
 ,得
,得
代入1,2式中得到范围。
(Ⅰ) 可设椭圆的标准方程为
则由长轴长等于4,即2a=4,所以a=2.又 ,所以
,所以 ,
,
又由于
所求椭圆C的标准方程为
(Ⅱ) 假设存在这样的直线 ,设
,设 ,MN的中点为
,MN的中点为
因为|ME|=|NE|所以MN EF所以
EF所以
(i)其中若 时,则K=0,显然直线
时,则K=0,显然直线 符合题意;
符合题意;
(ii)下面仅考虑 情形:
情形:
由 ,得,
,得,
 ,得
,得 ……② ……………………9分
……② ……………………9分
则 .
.
代入①式得,解得 ………………………………………12分
………………………………………12分
代入②式得 ,得
,得 .
.
综上(i)(ii)可知,存在这样的直线 ,其斜率k的取值范围是
,其斜率k的取值范围是
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com