
题目列表(包括答案和解析)
已知![]() 在区间
在区间![]() 上是增函数.
上是增函数.
(1)求实数![]() 的取值范围;
的取值范围;
(2)记(1)中实数![]() 的范围为集合A,且设关于
的范围为集合A,且设关于![]() 的方程
的方程![]() 的两个非零实根为
的两个非零实根为![]() .
.
①求![]() 的最大值;
的最大值;
②试问:是否存在实数m,使得不等式![]() 对于任意
对于任意![]() 及
及![]() 恒成立?若存在,求m的取值范围;若不存在,请说明理由.
恒成立?若存在,求m的取值范围;若不存在,请说明理由.
已知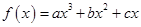 在区间
在区间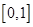 上是增函数,在区间
上是增函数,在区间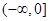 和
和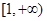 上是减函数,且
上是减函数,且
(1)求函数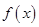 的解析式.
的解析式.
(2)若在区间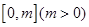 上恒有
上恒有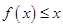 ,求实数
,求实数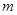 的取值范围.
的取值范围.
已知 在区间
在区间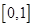 上是增函数,在区间
上是增函数,在区间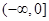 和
和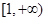 上是减函数,且
上是减函数,且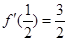
(1)求函数 的解析式.
的解析式.
(2)若在区间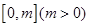 上恒有
上恒有 ,求实数
,求实数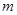 的取值范围.
的取值范围.
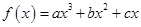 在区间
在区间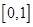 上是增函数,在区间
上是增函数,在区间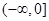 和
和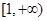 上是减函数,且
上是减函数,且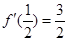
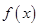 的解析式.
的解析式.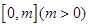 上恒有
上恒有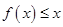 ,求实数
,求实数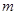 的取值范围.
的取值范围.已知![]() 在区间
在区间![]() 上是增函数。
上是增函数。
(Ⅰ)求实数![]() 的值所组成的集合
的值所组成的集合![]() ;
;
(Ⅱ)设关于![]() 的方程
的方程![]() 的两个根为
的两个根为![]() 、
、![]() ,若对任意
,若对任意![]() 及
及![]() ,不等式
,不等式
![]() 恒成立,求
恒成立,求![]() 的取值范围.
的取值范围.
一、选择题:本大题共10小题,每小题5分,共50分.
题号
1
2
3
4
5
6
7
8
9
10
答案
A
D
C
B
D
A
B
B
C
D
二、填空题:本大题7小题,每小题4分,共28分.
11、 ; 12、
; 12、  ; 13、
; 13、 ; 14、
; 14、 ; 15、
; 15、 ; 16、
; 16、 ;17、
;17、 。
。
三、解答题
18、(1)略 ……………………………………………………………………(7分)
(2) 就是二面角
就是二面角 的平面角,即
的平面角,即 ,
,
 …………………………………………………………………(9分)
…………………………………………………………………(9分)
取 中点
中点 ,则
,则 平面
平面 ,
,
 就是
就是 与平面
与平面 所成的角。 …………………………(11分)
所成的角。 …………………………(11分)
 ,
, ,
,
所以 与平面
与平面 所成的角的大小为
所成的角的大小为 。 …………………………(14分)
。 …………………………(14分)
(用向量方法,相应给分)
19、(1) ,
, ,
, …………(7分)
…………(7分)
(2) ,当
,当 时,
时, ;当
;当 时,
时,
 ,而
,而 ,
,
 ……………………………………………(14分)
……………………………………………(14分)
20、(1)当 ,当k=1时,
,当k=1时,
 ……………………………………… (7分)
……………………………………… (7分)
(2)由已知 ,又设
,又设 ,则
,则
 ,
,
知当 时,
时, 为增函数,则知
为增函数,则知 为增函数。…………………(14分)
为增函数。…………………(14分)
(用导数法相应给分)
21、.解:(1)、设 ,则
,则 ,
,
∵点P分 所成的比为
所成的比为 ∴
∴  ∴
∴ 
∴ 代入
代入 中,得
中,得 为P点的轨迹方程.
为P点的轨迹方程.
当 时,轨迹是圆. …………………………………………………(7分)
时,轨迹是圆. …………………………………………………(7分)
(2)、由题设知直线l的方程为 , 设
, 设
联立方程组 ,消去
,消去 得:
得:
∵ 方程组有两解 ∴  且
且 ∴
∴ 或
或 且
且
∵
 ∴
∴
又 ∵  ∴
∴  解得
解得 (舍去)或
(舍去)或
∴ 曲线C的方程是 ……………………………………………(14分)
……………………………………………(14分)
22、解(1) ………………………………………………(5分)
………………………………………………(5分)
猜想  , …………………………………………………………(7分)
, …………………………………………………………(7分)
证明(略) ……………………………………………………………………(10分)
(2) ,要使
,要使 恒成立,
恒成立,
 恒成立
恒成立
即 恒成立.
恒成立.
(i)当 为奇数时,即
为奇数时,即 恒成立, 又
恒成立, 又 的最小值为1,
的最小值为1,
(ii)当 为偶数时,即
为偶数时,即 恒成立, 又
恒成立, 又 的最大值为
的最大值为 ,
,
 即
即 ,又
,又 ,
, 为整数,
为整数,
∴ ,使得对任意
,使得对任意 ,都有
,都有 …………………………………( 16分)
…………………………………( 16分)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com