某校初二年级全体320名学生在电脑培训前后分别参加了一次水平相同的考试，考分都以同一标准划分成“不合格”、“合格”、“优秀”三个等级．为了了解电脑培训的效果，用抽签方式得到其中32名学生的两次考分等级．所绘制的统计图如图所示．

试结合图示信息回答下列问题：

(1)这32名学生培训前考分的中位数所在的等级是______，培训后考分的中位数所在的等级是______．

(2)这32名学生经过培训，考分等级“不合格”的百分比由_______下降到_______．

(3)估计该校整个初二年级中，培训后考分等级为“合格”与“优秀”的学生共有______名．

(4)你认为上述估计合理吗？理由是什么？

答：_____________________________；

理由是___________________________________．

某校初二年级全体320名学生在电脑培训前后分别参加了一次水平相同的考试，考分都以同一标准划分成“不合格”、“合格”、“优秀”三个等级．为了了解电脑培训的效果，用抽签方式得到其中32名学生的两次考分等级．所绘制的统计图如图所示．

(1)这32名学生培训前考分的中位数所在的等级是______，培训后考分的中位数所在的等级是______．

(2)这32名学生经过培训，考分等级“不合格”的百分比由_______下降到_______．

(3)估计该校整个初二年级中，培训后考分等级为“合格”与“优秀”的学生共有______名．

(4)你认为上述估计合理吗？理由是什么？

答：_____________________________；

理由是___________________________________．

若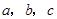是不全相等的实数，求证：．

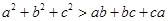证明过程如下：

，，，，

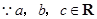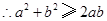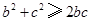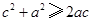又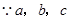不全相等，

以上三式至少有一个“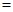”不成立，

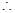将以上三式相加得，

．

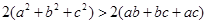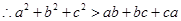此证法是（    ）

A．分析法       B．综合法       C．分析法与综合法并用       D．反证法

学习三角函数一章时，课堂上老师给出这样一个结论:当时，有恒成立，当老师把这个证明完成时，

(Ⅰ) 学生甲提出问题：能否在不等式的左边增加一个量，使不等号的方向得以改变？

下面请同学们证明：若，则 成立。

(Ⅱ) 当学生甲的问题完成时，学生乙提问：对于不等式是否也有相似的结论？

下面请同学们探讨：若，是否存在实数，使恒成立?如果存在,求出的一个值;如果不存在,请说明理由.

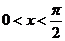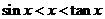学习三角函数一章时，课堂上老师给出这样一个结论:当时，有恒成立，当老师把这个证明完成时，

(Ⅰ) 学生甲提出问题：能否在不等式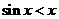的左边增加一个量，使不等号的方向得以改变？

下面请同学们证明：若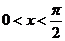，则 成立。

(Ⅱ) 当学生甲的问题完成时，学生乙提问：对于不等式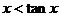是否也有相似的结论？

下面请同学们探讨：若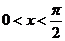，是否存在实数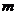，使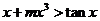恒成立?如果存在,求出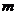的一个值;如果不存在,请说明理由.