
题目列表(包括答案和解析)
(选修4—1几何证明选讲)已知:直线AB过圆心O,交⊙O于AB,直线AF交⊙O于F(不与B重合),直线l与⊙O相切于C,交AB于E,且与AF垂直,垂足为G,连结AC
 求证:(1)
求证:(1)![]() (2)AC2=AE·AF
(2)AC2=AE·AF
23(选修4—4坐标系与参数方程选讲)以直角坐标系的原点O为极点,![]() 轴的正半轴为极轴,且两个坐标系取相等的单位长度.已知直线
轴的正半轴为极轴,且两个坐标系取相等的单位长度.已知直线![]() 经过点P(1,1),倾斜角
经过点P(1,1),倾斜角![]() .
.
(I)写出直线![]() 参数方程;
参数方程;
(II)设![]() 与圆
与圆![]() 相交于两点A、B,求点P到A、B两点的距离之积.
相交于两点A、B,求点P到A、B两点的距离之积.
24.选修4-5:不等式选讲
设函数![]() .
.
(Ⅰ)求不等式![]() 的解集;
的解集;
(Ⅱ)![]() ,使
,使![]() ,求实数
,求实数![]() 的取值范围.
的取值范围.
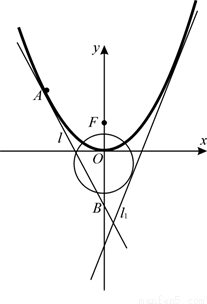
如图,已知直线 (
( )与抛物线
)与抛物线 :
: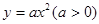 和圆
和圆 :
: 都相切,
都相切, 是
是 的焦点.
的焦点.
(Ⅰ)求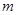 与
与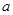 的值;
的值;
(Ⅱ)设 是
是 上的一动点,以
上的一动点,以 为切点作抛物线
为切点作抛物线 的切线
的切线 ,直线
,直线 交
交 轴于点
轴于点 ,以
,以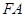 、
、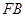 为邻边作平行四边形
为邻边作平行四边形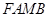 ,证明:点
,证明:点 在一条定直线上;
在一条定直线上;
(Ⅲ)在(Ⅱ)的条件下,记点 所在的定直线为
所在的定直线为 , 直线
, 直线 与
与 轴交点为
轴交点为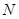 ,连接
,连接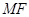 交抛物线
交抛物线 于
于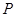 、
、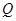 两点,求△
两点,求△ 的面积
的面积 的取值范围.
的取值范围.
【解析】第一问中利用圆 :
:
 的圆心为
的圆心为 ,半径
,半径 .由题设圆心到直线
.由题设圆心到直线 的距离
的距离 .
.
即 ,解得
,解得 (
( 舍去)
舍去)
设 与抛物线的相切点为
与抛物线的相切点为 ,又
,又 ,得
,得 ,
, .
.
代入直线方程得: ,∴
,∴ 所以
所以 ,
,
第二问中,由(Ⅰ)知抛物线 方程为
方程为 ,焦点
,焦点 . ………………(2分)
. ………………(2分)
设 ,由(Ⅰ)知以
,由(Ⅰ)知以 为切点的切线
为切点的切线 的方程为
的方程为 .
.
令 ,得切线
,得切线 交
交 轴的
轴的 点坐标为
点坐标为 所以
所以 ,
, , ∵四边形FAMB是以FA、FB为邻边作平行四边形
, ∵四边形FAMB是以FA、FB为邻边作平行四边形
∴ 因为
因为 是定点,所以点
是定点,所以点 在定直线
在定直线
第三问中,设直线 ,代入
,代入 得
得 结合韦达定理得到。
结合韦达定理得到。
解:(Ⅰ)由已知,圆 :
:
 的圆心为
的圆心为 ,半径
,半径 .由题设圆心到直线
.由题设圆心到直线 的距离
的距离 .
.
即 ,解得
,解得 (
( 舍去). …………………(2分)
舍去). …………………(2分)
设 与抛物线的相切点为
与抛物线的相切点为 ,又
,又 ,得
,得 ,
, .
.
代入直线方程得: ,∴
,∴ 所以
所以 ,
, .
……(2分)
.
……(2分)
(Ⅱ)由(Ⅰ)知抛物线 方程为
方程为 ,焦点
,焦点 . ………………(2分)
. ………………(2分)
设 ,由(Ⅰ)知以
,由(Ⅰ)知以 为切点的切线
为切点的切线 的方程为
的方程为 .
.
令 ,得切线
,得切线 交
交 轴的
轴的 点坐标为
点坐标为 所以
所以 ,
, , ∵四边形FAMB是以FA、FB为邻边作平行四边形,
, ∵四边形FAMB是以FA、FB为邻边作平行四边形,
∴ 因为
因为 是定点,所以点
是定点,所以点 在定直线
在定直线 上.…(2分)
上.…(2分)
(Ⅲ)设直线 ,代入
,代入 得
得 , ……)得
, ……)得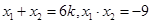 ,
…………………………… (2分)
,
…………………………… (2分)
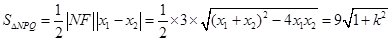 ,
,
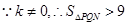 .
. △
△ 的面积
的面积 范围是
范围是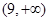
三棱柱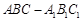 中,侧棱与底面垂直,
中,侧棱与底面垂直,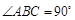 ,
,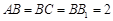 ,
,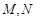 分别是
分别是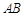 ,
, 的中点.
的中点.
(Ⅰ)求证: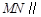 平面
平面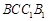 ;
;
(Ⅱ)求证: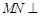 平面
平面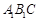 ;
;
(Ⅲ)求三棱锥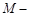
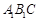 的体积.
的体积.
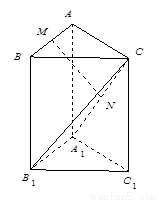
【解析】第一问利连结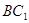 ,
,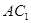 ,∵M,N是AB,
,∵M,N是AB, 的中点∴MN//
的中点∴MN//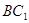 .
.
又∵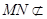 平面
平面 ,∴MN//平面
,∴MN//平面 .
. ----------4分
----------4分
⑵中年∵三棱柱ABC-A1B1C1中,侧棱与底面垂直,∴四边形 是正方形.∴
是正方形.∴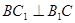 .∴
.∴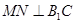 .连结
.连结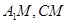 ,
,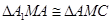 .
.
∴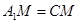 ,又N中
,又N中 的中点,∴
的中点,∴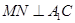 .
.
∵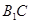 与
与 相交于点C,∴MN
相交于点C,∴MN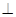 平面
平面 . --------------9分
. --------------9分
⑶中由⑵知MN是三棱锥M- 的高.在直角
的高.在直角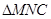 中,
中,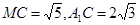 ,
,
∴MN=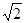 .又
.又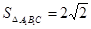 .
.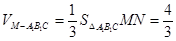 .得到结论。
.得到结论。
⑴连结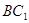 ,
,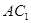 ,∵M,N是AB,
,∵M,N是AB, 的中点∴MN//
的中点∴MN//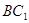 .
.
又∵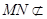 平面
平面 ,∴MN//平面
,∴MN//平面 .
. --------4分
--------4分
⑵∵三棱柱ABC-A1B1C1中,侧棱与底面垂直,
∴四边形 是正方形.∴
是正方形.∴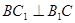 .
.
∴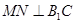 .连结
.连结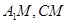 ,
,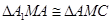 .
.
∴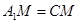 ,又N中
,又N中 的中点,∴
的中点,∴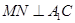 .
.
∵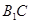 与
与 相交于点C,∴MN
相交于点C,∴MN 平面
平面 . --------------9分
. --------------9分
⑶由⑵知MN是三棱锥M- 的高.在直角
的高.在直角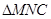 中,
中,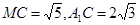 ,
,
∴MN=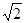 .又
.又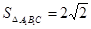 .
.
(选做题)本大题包括A,B,C,D共4小题,请从这4题中选做2小题. 每小题10分,共20分.请在答题卡上准确填涂题目标记. 解答时应写出文字说明、证明过程或演算步骤.
 A. 选修4-1:几何证明选讲
A. 选修4-1:几何证明选讲
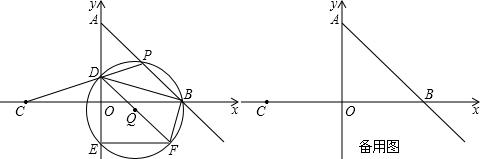
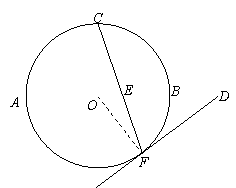
如图,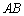 是⊙
是⊙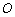 的直径,
的直径,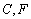 是⊙
是⊙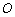 上的两点,
上的两点,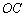 ⊥
⊥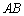 ,
,
过点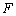 作⊙
作⊙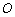 的切线FD交
的切线FD交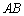 的延长线于点
的延长线于点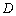 .连结
.连结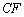 交
交
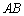 于点
于点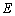 .
.
求证: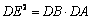 .
.
B. 选修4-2:矩阵与变换
求矩阵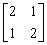 的特征值及对应的特征向量.
的特征值及对应的特征向量.
C. 选修4-4:坐标系与参数方程
已知曲线 的极坐标方程是
的极坐标方程是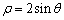 ,直线
,直线 的参数方程是
的参数方程是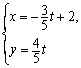 (
(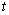 为参数).
为参数).
(1)将曲线 的极坐标方程化为直角坐标方程;
的极坐标方程化为直角坐标方程;
(2)设直线 与
与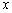 轴的交点是
轴的交点是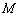 ,
,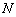 是曲线
是曲线 上一动点,求
上一动点,求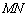 的最大值.
的最大值.
D.选修4-5:不等式选讲
设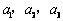 均为正数,且
均为正数,且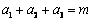 ,求证
,求证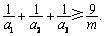
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com