
题目列表(包括答案和解析)
已知函数 .(
.( )
)
(1)若 在区间
在区间 上单调递增,求实数
上单调递增,求实数 的取值范围;
的取值范围;
(2)若在区间 上,函数
上,函数 的图象恒在曲线
的图象恒在曲线 下方,求
下方,求 的取值范围.
的取值范围.
【解析】第一问中,首先利用 在区间
在区间 上单调递增,则
上单调递增,则 在区间
在区间 上恒成立,然后分离参数法得到
上恒成立,然后分离参数法得到 ,进而得到范围;第二问中,在区间
,进而得到范围;第二问中,在区间 上,函数
上,函数 的图象恒在曲线
的图象恒在曲线 下方等价于
下方等价于 在区间
在区间 上恒成立.然后求解得到。
上恒成立.然后求解得到。
解:(1) 在区间
在区间 上单调递增,
上单调递增,
则 在区间
在区间 上恒成立. …………3分
上恒成立. …………3分
即 ,而当
,而当 时,
时, ,故
,故 .
…………5分
.
…………5分
所以 .
…………6分
.
…………6分
(2)令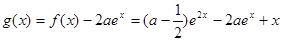 ,定义域为
,定义域为 .
.
在区间 上,函数
上,函数 的图象恒在曲线
的图象恒在曲线 下方等价于
下方等价于 在区间
在区间 上恒成立.
上恒成立.
∵ …………9分
…………9分
① 若 ,令
,令 ,得极值点
,得极值点 ,
, ,
,
当 ,即
,即 时,在(
时,在( ,+∞)上有
,+∞)上有 ,此时
,此时 在区间
在区间 上是增函数,并且在该区间上有
上是增函数,并且在该区间上有 ,不合题意;
,不合题意;
当 ,即
,即 时,同理可知,
时,同理可知, 在区间
在区间 上递增,
上递增,
有 ,也不合题意;
…………11分
,也不合题意;
…………11分
② 若 ,则有
,则有 ,此时在区间
,此时在区间 上恒有
上恒有 ,从而
,从而 在区间
在区间 上是减函数;
上是减函数;
要使 在此区间上恒成立,只须满足
在此区间上恒成立,只须满足
 ,
,
由此求得 的范围是
的范围是 . …………13分
. …………13分
综合①②可知,当 时,函数
时,函数 的图象恒在直线
的图象恒在直线 下方.
下方.
| 1 |
| x2+x-6 |
| 1 |
| 2 |
| 3 |
| π |
| 3 |
| π |
| 6 |
(本题满分16分)第(1)小题满分6分,第(2)小题满分5分,第(3)小题满分5分。
已知函数![]() 。
。
(1)当![]() 时,画出函数
时,画出函数![]() 的大致图像,并写出其单调递增区间;
的大致图像,并写出其单调递增区间;
(2)若函数![]() 在
在![]() 上是单调递减函数,求实数
上是单调递减函数,求实数![]() 的取值范围;
的取值范围;
(3)若不等式![]() 对
对![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
 |
(本题满分16分)第(1)小题满分6分,第(2)小题满分5分,第(3)小题满分5分。
已知函数![]() 。
。
(1)当![]() 时,画出函数
时,画出函数![]() 的大致图像,并写出其单调递增区间;
的大致图像,并写出其单调递增区间;
(2)若函数![]() 在
在![]() 上是单调递减函数,求实数
上是单调递减函数,求实数![]() 的取值范围;
的取值范围;
(3)若不等式![]() 对
对![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
 |
(本小题16分)
探究函数![]() 的最大值,并确定取得最大值时
的最大值,并确定取得最大值时![]() 的值.列表如下:
的值.列表如下:
|
| … | -0.5 | -1 | -1.5 | -1.7 | -1.9 | -2 | -2.1 | -2.2 | -2.3 | -3 | … |
|
| … | -8.5 | -5 | -4.17 | -4.05 | -4.005 | -4 | -4.005 | -4.02 | -4.04 | -4.3 | … |
请观察表中![]() 值随
值随![]() 值变化的特点,完成以下的问题.
值变化的特点,完成以下的问题.
(1)函数![]() 在区间 上为单调递增函数.当
在区间 上为单调递增函数.当![]() 时,
时,![]() .
.
(2)证明:函数![]() 在区间
在区间![]() 为单调递减函数.
为单调递减函数.
(3)思考:函数![]() 有最大值或最小值吗?如有,是多少?此时
有最大值或最小值吗?如有,是多少?此时![]() 为何值?(直接回答结果,不需证明).
为何值?(直接回答结果,不需证明).
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com