
题目列表(包括答案和解析)
函数 的图象(如图),则函数
的图象(如图),则函数 的单调递增区间是( )
的单调递增区间是( )

A. 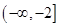 B.
B.

C.  D.
D.

函数 的导函数
的导函数 的图象如上图所示,则下列说法正确的是 ( )
的图象如上图所示,则下列说法正确的是 ( )
A、函数 在
在 内单调递减 B、函数
内单调递减 B、函数 在
在 内单调递增
内单调递增
C、函数 在
在 处取极大值 D、函数
处取极大值 D、函数 在
在 处取极小值
处取极小值

函数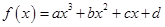 的图象(如图),则函数
的图象(如图),则函数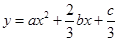 的单调递增区间是( )
的单调递增区间是( )
A.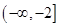 | B.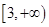 |
C.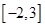 | D.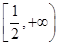 |
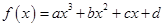 的图象(如图),则函数
的图象(如图),则函数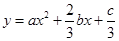 的单调递增区间是( )
的单调递增区间是( )
A.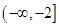 | B.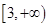 |
C.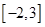 | D.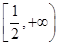 |
 函数f(x)=x3+bx2+cx+d图象如图,则函数y=x2+
函数f(x)=x3+bx2+cx+d图象如图,则函数y=x2+| 2 |
| 3 |
| c |
| 3 |
| A、(-∞,-2] | ||
| B、[3,+∞) | ||
| C、[-2,3] | ||
D、[
|
一、选择题:
1.C 2.A 3 .C 4.A 5.A 6.B 7.A 8.A 9.A 10.A 11.C 12.D
二、填空题:
13.12 14.
⒘⒚同理科
⒙(I)解:设数列{ }的公比为q,由
}的公比为q,由 可得
可得
解得a1=2,q=4.所以数列{ }的通项公式为
}的通项公式为 …………6分
…………6分
(II)解:由 ,得
,得
所以数列{ }是首项b1=1,公差d=2的等差数列.故
}是首项b1=1,公差d=2的等差数列.故 .
.
即数列{ }的前n项和Sn=n2.…………………………………
}的前n项和Sn=n2.…………………………………
⒛(I)解:只进行两局比赛,甲就取得胜利的概率为 …………4分
…………4分
(II)解:只进行两局比赛,比赛就结束的概率为: (III)解:甲取得比赛胜利共有三种情形:
(III)解:甲取得比赛胜利共有三种情形:
若甲胜乙,甲胜丙,则概率为 ;
;
若甲胜乙,甲负丙,则丙负乙,甲胜乙,概率为 ;
;
若甲负乙,则乙负丙,甲胜丙,甲胜乙,概率为
所以,甲获胜的概率为 …………
…………
21. (I)解:由点M是BN中点,又 ,
,
可知PM垂直平分BN.所以|PN|=|PB|,又|PA|+|PN|=|AN|,所以|PA|+|PB|=4.
由椭圆定义知,点P的轨迹是以A,B为焦点的椭圆.
设椭圆方程为 ,由
,由
可知动点P的轨迹方程为 …………………………6分
…………………………6分
(II)解:设点 的中点为Q,则
的中点为Q,则 ,
,
 ,
,
即以PB为直径的圆的圆心为 ,半径为
,半径为 ,
,
又圆 的圆心为O(0,0),半径r2=2,
的圆心为O(0,0),半径r2=2,
又
= ,故|OQ|=r2-r1,即两圆内切.…………………12分
,故|OQ|=r2-r1,即两圆内切.…………………12分
22. 解:(1)

当a>0时, 递增;
递增;
当a<时, 递减…………………………5分
递减…………………………5分
(2)当a>0时


0




+
0
-
0
+

增
极大值
减
极小值
增
此时,极大值为 …………7分
…………7分
当a<0时




0


-
0
+
0
-

减
极小值
增
极大值
减
此时,极大值为 …………9分
…………9分
因为线段AB与x轴有公共点
所以
解得 ……………………12分
……………………12分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com