题目列表(包括答案和解析)
（本小题满分12分）
甲、乙、丙三人参加了一家公司的招聘面试，面试合格者可正式签约，甲表示只要面试合格就签约.乙、丙则约定：两人面试都合格就一同签约，否则两人都不签约.设甲面试合格的概率为
，乙、丙面试合格的概率都是
，且面试是否合格互不影响．求：
（Ⅰ）至少有1人面试合格的概率；
（Ⅱ）签约人数
的分布列和数学期望．
（本小题满分12分）
甲，乙，丙三个同学同时报名参加某重点高校2012年自主招生．高考前自主招生的程序为审核材料和文化测试，只有审核过关后才能参加文化测试，文化测试合格者即可获得自主招生入选资格．因为甲，乙，丙三人各有优势，甲，乙，丙三人审核过关的概率分别为0.5，0.6，0.4，审核过关后，甲，乙，丙三人文化测试合格的概率分别为0.6，0.5，0.75．
（1）求甲，乙，丙三人中只有一人通过审核的概率；
（2）设甲，乙，丙三人中获得自主招生入选资格的人数为
，求随机变量的期望．
（本小题满分12分）
甲、乙、丙三台机床各自独立的加工同一种零件，已知甲、乙、丙三台机床加工的零件是一等品的概率分别为0.7、0.6、0.8，乙、丙两台机床加工的零件数相等，甲机床加工的零件数是乙机床加工的零件的二倍。
（1）从甲、乙、丙加工的零件中各取一件检验，示至少有一件一等品的概率；
（2）将三台机床加工的零件混合到一起，从中任意的抽取一件检验，求它是一等品的概率；
（3）将三台机床加工的零件混合到一起，从中任意的抽取4件检验，其中一等品的个数记为X，求EX。
（本小题满分12分）
甲，乙，丙三位学生独立地解同一道题，甲做对的概率为
，乙，丙做对的概率分别为
，
(＞)，且三位学生是否做对相互独立.记
为这三位学生中做对该题的人数，其分布列为：
|
|
0 |
1 |
2 |
3 |
|
|
|
|
|
|
（1) 求至少有一位学生做对该题的概率；
（2) 求，的值；
（3) 求的数学期望.
（本小题满分12分）
甲、乙、丙三人进行某项比赛，每局有两人参加，没有平局，在一局比赛中甲胜乙的概率为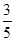
，甲胜丙的概
，乙胜丙的概率为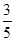，比赛的规则是先由甲和乙进行第一局的比赛，然后每局的获胜者与未参加此局比赛的人进行下一局的比赛，在比赛中，有人获胜两局就算取得比赛的胜利，比赛结束
网]
一、选择题：
1．C 2．A 3 .C 4．A 5．A 6．B 7．A 8．A 9．A 10．A 11.C 12.D
二、填空题：
13．12 14．
⒘⒚同理科
⒙（I）解：设数列{
}的公比为q，由
可得
解得a1=2，q=4.所以数列{}的通项公式为
…………6分
（II）解：由
，得
所以数列{
}是首项b1=1，公差d=2的等差数列.故
.
即数列{}的前n项和Sn=n2.…………………………………
⒛（I）解：只进行两局比赛，甲就取得胜利的概率为
…………4分
（II）解：只进行两局比赛，比赛就结束的概率为：
（III）解：甲取得比赛胜利共有三种情形：
若甲胜乙，甲胜丙，则概率为
；
若甲胜乙，甲负丙，则丙负乙，甲胜乙，概率为
；
若甲负乙，则乙负丙，甲胜丙，甲胜乙，概率为
所以，甲获胜的概率为
…………
21. （I）解：由点M是BN中点，又
，
可知PM垂直平分BN.所以|PN|=|PB|，又|PA|+|PN|=|AN|，所以|PA|+|PB|=4.
由椭圆定义知，点P的轨迹是以A，B为焦点的椭圆.
设椭圆方程为
，由
可知动点P的轨迹方程为
…………………………6分
（II）解：设点
的中点为Q，则
，
，
即以PB为直径的圆的圆心为
，半径为
，
又圆
的圆心为O（0，0），半径r2=2，
又
=
，故|OQ|=r2－r1，即两圆内切.…………………12分
22. 解：（1）
当a>0时，
递增；
当a<时，
递减…………………………5分
（2）当a>0时
0
+
0
－
0
+
增
极大值
减
极小值
增
此时，极大值为
…………7分
当a<0时
0
－
0
+
0
－
减
极小值
增
极大值
减
此时，极大值为
…………9分
因为线段AB与x轴有公共点
所以
解得
……………………12分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
