
题目列表(包括答案和解析)
在一次研究性学习中,老师给出函数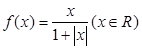 ,三位同学甲、乙、丙在研究此函数时给出命题:
,三位同学甲、乙、丙在研究此函数时给出命题:
甲:函数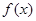 的值域为
的值域为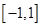 ;
;
乙:若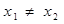 ,则一定有
,则一定有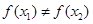 ;
;
丙:若规定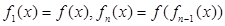 ,则
,则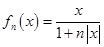 对任意
对任意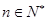 恒成立.
恒成立.
你认为上述三个命题中正确的个数有( )
A.0个 B.1个 C.2个 D.3个
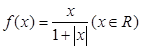 ,三位同学甲、乙、丙在研究此函数时给出命题:
,三位同学甲、乙、丙在研究此函数时给出命题: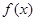 的值域为
的值域为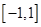 ;
;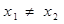 ,则一定有
,则一定有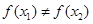 ;
;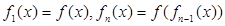 ,则
,则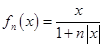 对任意
对任意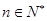 恒成立.
恒成立.| A.0个 | B.1个 | C.2个 | D.3个 |
一次研究性课堂上,老师给出函数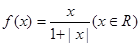 ,三位同学甲、乙、丙在研究此函数时分别给出命题:
,三位同学甲、乙、丙在研究此函数时分别给出命题:
甲:函数f (x)的值域为(-1,1);
乙:若x1≠x2,则一定有f (x1)≠f (x2);
丙:若规定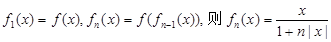 对任意
对任意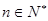 恒成立.
恒成立.
你认为上述三个命题中正确的个数有( )
A.0个 B.1个 C.2个 D.3个
一次研究性课堂上,老师给出函数![]() ,三位同学甲、乙、丙在研究此函数时分别给出命题:
,三位同学甲、乙、丙在研究此函数时分别给出命题:
甲:函数f (x)的值域为(-1,1);
乙:若x1≠x2,则一定有f (x1)≠f (x2);
丙:若规定![]() 对任意
对任意![]() 恒成立.
恒成立.
你认为上述三个命题中正确的个数有 ( )
A.0个 B.1个 C.2个 D.3个
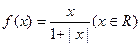 ,三位同学甲、乙、丙在研究此函数时分别给出命题:
,三位同学甲、乙、丙在研究此函数时分别给出命题: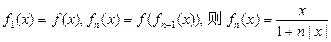 对任意
对任意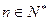 恒成立.
恒成立.| A.0个 | B.1个 | C.2个 | D.3个 |
1. 4 2. /file:///E:\cooco.net.cn\docfiles\down\test\down\e0c9b9362434b193df3f29a00e3c9c0c.zip\66802\江苏省2009届高三数学高考模拟试题精选(27套)\2009届江苏省东台中学高三第一学期期末数学考试试题.files\image181.gif) 3.
3./file:///E:\cooco.net.cn\docfiles\down\test\down\e0c9b9362434b193df3f29a00e3c9c0c.zip\66802\江苏省2009届高三数学高考模拟试题精选(27套)\2009届江苏省东台中学高三第一学期期末数学考试试题.files\image183.gif) 3.
3. /file:///E:\cooco.net.cn\docfiles\down\test\down\e0c9b9362434b193df3f29a00e3c9c0c.zip\66802\江苏省2009届高三数学高考模拟试题精选(27套)\2009届江苏省东台中学高三第一学期期末数学考试试题.files\image185.gif) 4.
4. /file:///E:\cooco.net.cn\docfiles\down\test\down\e0c9b9362434b193df3f29a00e3c9c0c.zip\66802\江苏省2009届高三数学高考模拟试题精选(27套)\2009届江苏省东台中学高三第一学期期末数学考试试题.files\image187.gif) 5.
5. /file:///E:\cooco.net.cn\docfiles\down\test\down\e0c9b9362434b193df3f29a00e3c9c0c.zip\66802\江苏省2009届高三数学高考模拟试题精选(27套)\2009届江苏省东台中学高三第一学期期末数学考试试题.files\image181.gif) 6.
6. /file:///E:\cooco.net.cn\docfiles\down\test\down\e0c9b9362434b193df3f29a00e3c9c0c.zip\66802\江苏省2009届高三数学高考模拟试题精选(27套)\2009届江苏省东台中学高三第一学期期末数学考试试题.files\image189.gif)
7. /file:///E:\cooco.net.cn\docfiles\down\test\down\e0c9b9362434b193df3f29a00e3c9c0c.zip\66802\江苏省2009届高三数学高考模拟试题精选(27套)\2009届江苏省东台中学高三第一学期期末数学考试试题.files\image191.gif) 8. 3 9.32 10.
8. 3 9.32 10. /file:///E:\cooco.net.cn\docfiles\down\test\down\e0c9b9362434b193df3f29a00e3c9c0c.zip\66802\江苏省2009届高三数学高考模拟试题精选(27套)\2009届江苏省东台中学高三第一学期期末数学考试试题.files\image193.gif) 11. 它的前
11. 它的前/file:///E:\cooco.net.cn\docfiles\down\test\down\e0c9b9362434b193df3f29a00e3c9c0c.zip\66802\江苏省2009届高三数学高考模拟试题精选(27套)\2009届江苏省东台中学高三第一学期期末数学考试试题.files\image062.gif) 项乘积为
项乘积为/file:///E:\cooco.net.cn\docfiles\down\test\down\e0c9b9362434b193df3f29a00e3c9c0c.zip\66802\江苏省2009届高三数学高考模拟试题精选(27套)\2009届江苏省东台中学高三第一学期期末数学考试试题.files\image195.gif) ,若
,若/file:///E:\cooco.net.cn\docfiles\down\test\down\e0c9b9362434b193df3f29a00e3c9c0c.zip\66802\江苏省2009届高三数学高考模拟试题精选(27套)\2009届江苏省东台中学高三第一学期期末数学考试试题.files\image197.gif) ,则
,则/file:///E:\cooco.net.cn\docfiles\down\test\down\e0c9b9362434b193df3f29a00e3c9c0c.zip\66802\江苏省2009届高三数学高考模拟试题精选(27套)\2009届江苏省东台中学高三第一学期期末数学考试试题.files\image199.gif)
12. /file:///E:\cooco.net.cn\docfiles\down\test\down\e0c9b9362434b193df3f29a00e3c9c0c.zip\66802\江苏省2009届高三数学高考模拟试题精选(27套)\2009届江苏省东台中学高三第一学期期末数学考试试题.files\image201.gif) 13. [1,1+
13. [1,1+/file:///E:\cooco.net.cn\docfiles\down\test\down\e0c9b9362434b193df3f29a00e3c9c0c.zip\66802\江苏省2009届高三数学高考模拟试题精选(27套)\2009届江苏省东台中学高三第一学期期末数学考试试题.files\image203.gif) ] 14. 4
] 14. 4
15.解:(1)当/file:///E:\cooco.net.cn\docfiles\down\test\down\e0c9b9362434b193df3f29a00e3c9c0c.zip\66802\江苏省2009届高三数学高考模拟试题精选(27套)\2009届江苏省东台中学高三第一学期期末数学考试试题.files\image099.gif) 时,
时,/file:///E:\cooco.net.cn\docfiles\down\test\down\e0c9b9362434b193df3f29a00e3c9c0c.zip\66802\江苏省2009届高三数学高考模拟试题精选(27套)\2009届江苏省东台中学高三第一学期期末数学考试试题.files\image206.gif) ,
,
∵/file:///E:\cooco.net.cn\docfiles\down\test\down\e0c9b9362434b193df3f29a00e3c9c0c.zip\66802\江苏省2009届高三数学高考模拟试题精选(27套)\2009届江苏省东台中学高三第一学期期末数学考试试题.files\image208.gif)
/file:///E:\cooco.net.cn\docfiles\down\test\down\e0c9b9362434b193df3f29a00e3c9c0c.zip\66802\江苏省2009届高三数学高考模拟试题精选(27套)\2009届江苏省东台中学高三第一学期期末数学考试试题.files\image210.gif) ,∴
,∴/file:///E:\cooco.net.cn\docfiles\down\test\down\e0c9b9362434b193df3f29a00e3c9c0c.zip\66802\江苏省2009届高三数学高考模拟试题精选(27套)\2009届江苏省东台中学高三第一学期期末数学考试试题.files\image020.gif) 在
在/file:///E:\cooco.net.cn\docfiles\down\test\down\e0c9b9362434b193df3f29a00e3c9c0c.zip\66802\江苏省2009届高三数学高考模拟试题精选(27套)\2009届江苏省东台中学高三第一学期期末数学考试试题.files\image102.gif) 上是减函数.
上是减函数.
(2)∵/file:///E:\cooco.net.cn\docfiles\down\test\down\e0c9b9362434b193df3f29a00e3c9c0c.zip\66802\江苏省2009届高三数学高考模拟试题精选(27套)\2009届江苏省东台中学高三第一学期期末数学考试试题.files\image104.gif) 不等式
不等式/file:///E:\cooco.net.cn\docfiles\down\test\down\e0c9b9362434b193df3f29a00e3c9c0c.zip\66802\江苏省2009届高三数学高考模拟试题精选(27套)\2009届江苏省东台中学高三第一学期期末数学考试试题.files\image106.gif) 恒成立,即
恒成立,即/file:///E:\cooco.net.cn\docfiles\down\test\down\e0c9b9362434b193df3f29a00e3c9c0c.zip\66802\江苏省2009届高三数学高考模拟试题精选(27套)\2009届江苏省东台中学高三第一学期期末数学考试试题.files\image104.gif) 不等式
不等式/file:///E:\cooco.net.cn\docfiles\down\test\down\e0c9b9362434b193df3f29a00e3c9c0c.zip\66802\江苏省2009届高三数学高考模拟试题精选(27套)\2009届江苏省东台中学高三第一学期期末数学考试试题.files\image217.gif) 恒成立,
恒成立,
∴/file:///E:\cooco.net.cn\docfiles\down\test\down\e0c9b9362434b193df3f29a00e3c9c0c.zip\66802\江苏省2009届高三数学高考模拟试题精选(27套)\2009届江苏省东台中学高三第一学期期末数学考试试题.files\image104.gif) 不等式
不等式/file:///E:\cooco.net.cn\docfiles\down\test\down\e0c9b9362434b193df3f29a00e3c9c0c.zip\66802\江苏省2009届高三数学高考模拟试题精选(27套)\2009届江苏省东台中学高三第一学期期末数学考试试题.files\image220.gif) 恒成立. 当
恒成立. 当/file:///E:\cooco.net.cn\docfiles\down\test\down\e0c9b9362434b193df3f29a00e3c9c0c.zip\66802\江苏省2009届高三数学高考模拟试题精选(27套)\2009届江苏省东台中学高三第一学期期末数学考试试题.files\image222.gif) 时,
时,/file:///E:\cooco.net.cn\docfiles\down\test\down\e0c9b9362434b193df3f29a00e3c9c0c.zip\66802\江苏省2009届高三数学高考模拟试题精选(27套)\2009届江苏省东台中学高三第一学期期末数学考试试题.files\image104.gif)
/file:///E:\cooco.net.cn\docfiles\down\test\down\e0c9b9362434b193df3f29a00e3c9c0c.zip\66802\江苏省2009届高三数学高考模拟试题精选(27套)\2009届江苏省东台中学高三第一学期期末数学考试试题.files\image225.gif) 不恒成立;
不恒成立;
当/file:///E:\cooco.net.cn\docfiles\down\test\down\e0c9b9362434b193df3f29a00e3c9c0c.zip\66802\江苏省2009届高三数学高考模拟试题精选(27套)\2009届江苏省东台中学高三第一学期期末数学考试试题.files\image227.gif) 时,
时,/file:///E:\cooco.net.cn\docfiles\down\test\down\e0c9b9362434b193df3f29a00e3c9c0c.zip\66802\江苏省2009届高三数学高考模拟试题精选(27套)\2009届江苏省东台中学高三第一学期期末数学考试试题.files\image104.gif) 不等式
不等式/file:///E:\cooco.net.cn\docfiles\down\test\down\e0c9b9362434b193df3f29a00e3c9c0c.zip\66802\江苏省2009届高三数学高考模拟试题精选(27套)\2009届江苏省东台中学高三第一学期期末数学考试试题.files\image220.gif) 恒成立,即
恒成立,即/file:///E:\cooco.net.cn\docfiles\down\test\down\e0c9b9362434b193df3f29a00e3c9c0c.zip\66802\江苏省2009届高三数学高考模拟试题精选(27套)\2009届江苏省东台中学高三第一学期期末数学考试试题.files\image231.gif) ,∴
,∴/file:///E:\cooco.net.cn\docfiles\down\test\down\e0c9b9362434b193df3f29a00e3c9c0c.zip\66802\江苏省2009届高三数学高考模拟试题精选(27套)\2009届江苏省东台中学高三第一学期期末数学考试试题.files\image233.gif) .
.
当/file:///E:\cooco.net.cn\docfiles\down\test\down\e0c9b9362434b193df3f29a00e3c9c0c.zip\66802\江苏省2009届高三数学高考模拟试题精选(27套)\2009届江苏省东台中学高三第一学期期末数学考试试题.files\image235.gif) 时,
时,/file:///E:\cooco.net.cn\docfiles\down\test\down\e0c9b9362434b193df3f29a00e3c9c0c.zip\66802\江苏省2009届高三数学高考模拟试题精选(27套)\2009届江苏省东台中学高三第一学期期末数学考试试题.files\image104.gif) 不等式
不等式/file:///E:\cooco.net.cn\docfiles\down\test\down\e0c9b9362434b193df3f29a00e3c9c0c.zip\66802\江苏省2009届高三数学高考模拟试题精选(27套)\2009届江苏省东台中学高三第一学期期末数学考试试题.files\image238.gif) 不恒成立. 综上,
不恒成立. 综上,/file:///E:\cooco.net.cn\docfiles\down\test\down\e0c9b9362434b193df3f29a00e3c9c0c.zip\66802\江苏省2009届高三数学高考模拟试题精选(27套)\2009届江苏省东台中学高三第一学期期末数学考试试题.files\image108.gif) 的取值范围是
的取值范围是/file:///E:\cooco.net.cn\docfiles\down\test\down\e0c9b9362434b193df3f29a00e3c9c0c.zip\66802\江苏省2009届高三数学高考模拟试题精选(27套)\2009届江苏省东台中学高三第一学期期末数学考试试题.files\image241.gif) .
.
16.解:(1) /file:///E:\cooco.net.cn\docfiles\down\test\down\e0c9b9362434b193df3f29a00e3c9c0c.zip\66802\江苏省2009届高三数学高考模拟试题精选(27套)\2009届江苏省东台中学高三第一学期期末数学考试试题.files\image243.gif)
/file:///E:\cooco.net.cn\docfiles\down\test\down\e0c9b9362434b193df3f29a00e3c9c0c.zip\66802\江苏省2009届高三数学高考模拟试题精选(27套)\2009届江苏省东台中学高三第一学期期末数学考试试题.files\image245.gif)
/file:///E:\cooco.net.cn\docfiles\down\test\down\e0c9b9362434b193df3f29a00e3c9c0c.zip\66802\江苏省2009届高三数学高考模拟试题精选(27套)\2009届江苏省东台中学高三第一学期期末数学考试试题.files\image247.gif)
/file:///E:\cooco.net.cn\docfiles\down\test\down\e0c9b9362434b193df3f29a00e3c9c0c.zip\66802\江苏省2009届高三数学高考模拟试题精选(27套)\2009届江苏省东台中学高三第一学期期末数学考试试题.files\image245.gif)
/file:///E:\cooco.net.cn\docfiles\down\test\down\e0c9b9362434b193df3f29a00e3c9c0c.zip\66802\江苏省2009届高三数学高考模拟试题精选(27套)\2009届江苏省东台中学高三第一学期期末数学考试试题.files\image249.gif)
/file:///E:\cooco.net.cn\docfiles\down\test\down\e0c9b9362434b193df3f29a00e3c9c0c.zip\66802\江苏省2009届高三数学高考模拟试题精选(27套)\2009届江苏省东台中学高三第一学期期末数学考试试题.files\image245.gif)
/file:///E:\cooco.net.cn\docfiles\down\test\down\e0c9b9362434b193df3f29a00e3c9c0c.zip\66802\江苏省2009届高三数学高考模拟试题精选(27套)\2009届江苏省东台中学高三第一学期期末数学考试试题.files\image251.gif)
(2)/file:///E:\cooco.net.cn\docfiles\down\test\down\e0c9b9362434b193df3f29a00e3c9c0c.zip\66802\江苏省2009届高三数学高考模拟试题精选(27套)\2009届江苏省东台中学高三第一学期期末数学考试试题.files\image253.gif)
/file:///E:\cooco.net.cn\docfiles\down\test\down\e0c9b9362434b193df3f29a00e3c9c0c.zip\66802\江苏省2009届高三数学高考模拟试题精选(27套)\2009届江苏省东台中学高三第一学期期末数学考试试题.files\image255.gif) ,
,/file:///E:\cooco.net.cn\docfiles\down\test\down\e0c9b9362434b193df3f29a00e3c9c0c.zip\66802\江苏省2009届高三数学高考模拟试题精选(27套)\2009届江苏省东台中学高三第一学期期末数学考试试题.files\image257.gif) 20
20
由/file:///E:\cooco.net.cn\docfiles\down\test\down\e0c9b9362434b193df3f29a00e3c9c0c.zip\66802\江苏省2009届高三数学高考模拟试题精选(27套)\2009届江苏省东台中学高三第一学期期末数学考试试题.files\image259.gif) 及
及/file:///E:\cooco.net.cn\docfiles\down\test\down\e0c9b9362434b193df3f29a00e3c9c0c.zip\66802\江苏省2009届高三数学高考模拟试题精选(27套)\2009届江苏省东台中学高三第一学期期末数学考试试题.files\image261.gif) 20与
20与/file:///E:\cooco.net.cn\docfiles\down\test\down\e0c9b9362434b193df3f29a00e3c9c0c.zip\66802\江苏省2009届高三数学高考模拟试题精选(27套)\2009届江苏省东台中学高三第一学期期末数学考试试题.files\image058.gif) =3解得b=4,c=5或b=5,c= 4
=3解得b=4,c=5或b=5,c= 4
(3)设D到三边的距离分别为x、y、z,则/file:///E:\cooco.net.cn\docfiles\down\test\down\e0c9b9362434b193df3f29a00e3c9c0c.zip\66802\江苏省2009届高三数学高考模拟试题精选(27套)\2009届江苏省东台中学高三第一学期期末数学考试试题.files\image263.gif)
/file:///E:\cooco.net.cn\docfiles\down\test\down\e0c9b9362434b193df3f29a00e3c9c0c.zip\66802\江苏省2009届高三数学高考模拟试题精选(27套)\2009届江苏省东台中学高三第一学期期末数学考试试题.files\image265.gif) 又x、y满足
又x、y满足/file:///E:\cooco.net.cn\docfiles\down\test\down\e0c9b9362434b193df3f29a00e3c9c0c.zip\66802\江苏省2009届高三数学高考模拟试题精选(27套)\2009届江苏省东台中学高三第一学期期末数学考试试题.files\image267.gif)
画出不等式表示的平面区域得:/file:///E:\cooco.net.cn\docfiles\down\test\down\e0c9b9362434b193df3f29a00e3c9c0c.zip\66802\江苏省2009届高三数学高考模拟试题精选(27套)\2009届江苏省东台中学高三第一学期期末数学考试试题.files\image269.gif)
17. (Ⅰ)证明:连结/file:///E:\cooco.net.cn\docfiles\down\test\down\e0c9b9362434b193df3f29a00e3c9c0c.zip\66802\江苏省2009届高三数学高考模拟试题精选(27套)\2009届江苏省东台中学高三第一学期期末数学考试试题.files\image271.gif) ,则
,则/file:///E:\cooco.net.cn\docfiles\down\test\down\e0c9b9362434b193df3f29a00e3c9c0c.zip\66802\江苏省2009届高三数学高考模拟试题精选(27套)\2009届江苏省东台中学高三第一学期期末数学考试试题.files\image271.gif) //
///file:///E:\cooco.net.cn\docfiles\down\test\down\e0c9b9362434b193df3f29a00e3c9c0c.zip\66802\江苏省2009届高三数学高考模拟试题精选(27套)\2009届江苏省东台中学高三第一学期期末数学考试试题.files\image273.gif) , …………1分
, …………1分
∵/file:///E:\cooco.net.cn\docfiles\down\test\down\e0c9b9362434b193df3f29a00e3c9c0c.zip\66802\江苏省2009届高三数学高考模拟试题精选(27套)\2009届江苏省东台中学高三第一学期期末数学考试试题.files\image275.gif) 是正方形,∴
是正方形,∴/file:///E:\cooco.net.cn\docfiles\down\test\down\e0c9b9362434b193df3f29a00e3c9c0c.zip\66802\江苏省2009届高三数学高考模拟试题精选(27套)\2009届江苏省东台中学高三第一学期期末数学考试试题.files\image277.gif) .∵
.∵/file:///E:\cooco.net.cn\docfiles\down\test\down\e0c9b9362434b193df3f29a00e3c9c0c.zip\66802\江苏省2009届高三数学高考模拟试题精选(27套)\2009届江苏省东台中学高三第一学期期末数学考试试题.files\image279.gif) 面
面/file:///E:\cooco.net.cn\docfiles\down\test\down\e0c9b9362434b193df3f29a00e3c9c0c.zip\66802\江苏省2009届高三数学高考模拟试题精选(27套)\2009届江苏省东台中学高三第一学期期末数学考试试题.files\image275.gif) ,∴
,∴/file:///E:\cooco.net.cn\docfiles\down\test\down\e0c9b9362434b193df3f29a00e3c9c0c.zip\66802\江苏省2009届高三数学高考模拟试题精选(27套)\2009届江苏省东台中学高三第一学期期末数学考试试题.files\image282.gif) .
.
又/file:///E:\cooco.net.cn\docfiles\down\test\down\e0c9b9362434b193df3f29a00e3c9c0c.zip\66802\江苏省2009届高三数学高考模拟试题精选(27套)\2009届江苏省东台中学高三第一学期期末数学考试试题.files\image284.gif) ,∴
,∴/file:///E:\cooco.net.cn\docfiles\down\test\down\e0c9b9362434b193df3f29a00e3c9c0c.zip\66802\江苏省2009届高三数学高考模拟试题精选(27套)\2009届江苏省东台中学高三第一学期期末数学考试试题.files\image286.gif) 面
面/file:///E:\cooco.net.cn\docfiles\down\test\down\e0c9b9362434b193df3f29a00e3c9c0c.zip\66802\江苏省2009届高三数学高考模拟试题精选(27套)\2009届江苏省东台中学高三第一学期期末数学考试试题.files\image288.gif) . ………………4分
. ………………4分
∵/file:///E:\cooco.net.cn\docfiles\down\test\down\e0c9b9362434b193df3f29a00e3c9c0c.zip\66802\江苏省2009届高三数学高考模拟试题精选(27套)\2009届江苏省东台中学高三第一学期期末数学考试试题.files\image290.gif) 面
面/file:///E:\cooco.net.cn\docfiles\down\test\down\e0c9b9362434b193df3f29a00e3c9c0c.zip\66802\江苏省2009届高三数学高考模拟试题精选(27套)\2009届江苏省东台中学高三第一学期期末数学考试试题.files\image288.gif) ,∴
,∴/file:///E:\cooco.net.cn\docfiles\down\test\down\e0c9b9362434b193df3f29a00e3c9c0c.zip\66802\江苏省2009届高三数学高考模拟试题精选(27套)\2009届江苏省东台中学高三第一学期期末数学考试试题.files\image292.gif) ,
,
∴/file:///E:\cooco.net.cn\docfiles\down\test\down\e0c9b9362434b193df3f29a00e3c9c0c.zip\66802\江苏省2009届高三数学高考模拟试题精选(27套)\2009届江苏省东台中学高三第一学期期末数学考试试题.files\image294.gif) . …………………………………………5分
. …………………………………………5分
/file:///E:\cooco.net.cn\docfiles\down\test\down\e0c9b9362434b193df3f29a00e3c9c0c.zip\66802\江苏省2009届高三数学高考模拟试题精选(27套)\2009届江苏省东台中学高三第一学期期末数学考试试题.files\image295.gif) (Ⅱ)证明:作
(Ⅱ)证明:作/file:///E:\cooco.net.cn\docfiles\down\test\down\e0c9b9362434b193df3f29a00e3c9c0c.zip\66802\江苏省2009届高三数学高考模拟试题精选(27套)\2009届江苏省东台中学高三第一学期期末数学考试试题.files\image297.gif) 的中点F,连结
的中点F,连结/file:///E:\cooco.net.cn\docfiles\down\test\down\e0c9b9362434b193df3f29a00e3c9c0c.zip\66802\江苏省2009届高三数学高考模拟试题精选(27套)\2009届江苏省东台中学高三第一学期期末数学考试试题.files\image299.gif) .
.
∵/file:///E:\cooco.net.cn\docfiles\down\test\down\e0c9b9362434b193df3f29a00e3c9c0c.zip\66802\江苏省2009届高三数学高考模拟试题精选(27套)\2009届江苏省东台中学高三第一学期期末数学考试试题.files\image301.gif) 是
是/file:///E:\cooco.net.cn\docfiles\down\test\down\e0c9b9362434b193df3f29a00e3c9c0c.zip\66802\江苏省2009届高三数学高考模拟试题精选(27套)\2009届江苏省东台中学高三第一学期期末数学考试试题.files\image303.gif) 的中点,∴
的中点,∴/file:///E:\cooco.net.cn\docfiles\down\test\down\e0c9b9362434b193df3f29a00e3c9c0c.zip\66802\江苏省2009届高三数学高考模拟试题精选(27套)\2009届江苏省东台中学高三第一学期期末数学考试试题.files\image305.gif)
/file:///E:\cooco.net.cn\docfiles\down\test\down\e0c9b9362434b193df3f29a00e3c9c0c.zip\66802\江苏省2009届高三数学高考模拟试题精选(27套)\2009届江苏省东台中学高三第一学期期末数学考试试题.files\image307.jpg)
/file:///E:\cooco.net.cn\docfiles\down\test\down\e0c9b9362434b193df3f29a00e3c9c0c.zip\66802\江苏省2009届高三数学高考模拟试题精选(27套)\2009届江苏省东台中学高三第一学期期末数学考试试题.files\image309.gif) ,
,
∴四边形/file:///E:\cooco.net.cn\docfiles\down\test\down\e0c9b9362434b193df3f29a00e3c9c0c.zip\66802\江苏省2009届高三数学高考模拟试题精选(27套)\2009届江苏省东台中学高三第一学期期末数学考试试题.files\image311.gif) 是平行四边形,∴
是平行四边形,∴ /file:///E:\cooco.net.cn\docfiles\down\test\down\e0c9b9362434b193df3f29a00e3c9c0c.zip\66802\江苏省2009届高三数学高考模拟试题精选(27套)\2009届江苏省东台中学高三第一学期期末数学考试试题.files\image313.gif) . ………7分
. ………7分
∵/file:///E:\cooco.net.cn\docfiles\down\test\down\e0c9b9362434b193df3f29a00e3c9c0c.zip\66802\江苏省2009届高三数学高考模拟试题精选(27套)\2009届江苏省东台中学高三第一学期期末数学考试试题.files\image315.gif) 是
是/file:///E:\cooco.net.cn\docfiles\down\test\down\e0c9b9362434b193df3f29a00e3c9c0c.zip\66802\江苏省2009届高三数学高考模拟试题精选(27套)\2009届江苏省东台中学高三第一学期期末数学考试试题.files\image303.gif) 的中点,∴
的中点,∴/file:///E:\cooco.net.cn\docfiles\down\test\down\e0c9b9362434b193df3f29a00e3c9c0c.zip\66802\江苏省2009届高三数学高考模拟试题精选(27套)\2009届江苏省东台中学高三第一学期期末数学考试试题.files\image317.gif) ,
,
又/file:///E:\cooco.net.cn\docfiles\down\test\down\e0c9b9362434b193df3f29a00e3c9c0c.zip\66802\江苏省2009届高三数学高考模拟试题精选(27套)\2009届江苏省东台中学高三第一学期期末数学考试试题.files\image319.gif) ,∴
,∴/file:///E:\cooco.net.cn\docfiles\down\test\down\e0c9b9362434b193df3f29a00e3c9c0c.zip\66802\江苏省2009届高三数学高考模拟试题精选(27套)\2009届江苏省东台中学高三第一学期期末数学考试试题.files\image321.gif) .
.
∴四边形/file:///E:\cooco.net.cn\docfiles\down\test\down\e0c9b9362434b193df3f29a00e3c9c0c.zip\66802\江苏省2009届高三数学高考模拟试题精选(27套)\2009届江苏省东台中学高三第一学期期末数学考试试题.files\image323.gif) 是平行四边形,
是平行四边形,/file:///E:\cooco.net.cn\docfiles\down\test\down\e0c9b9362434b193df3f29a00e3c9c0c.zip\66802\江苏省2009届高三数学高考模拟试题精选(27套)\2009届江苏省东台中学高三第一学期期末数学考试试题.files\image325.gif) //
///file:///E:\cooco.net.cn\docfiles\down\test\down\e0c9b9362434b193df3f29a00e3c9c0c.zip\66802\江苏省2009届高三数学高考模拟试题精选(27套)\2009届江苏省东台中学高三第一学期期末数学考试试题.files\image327.gif) ,
,
∵/file:///E:\cooco.net.cn\docfiles\down\test\down\e0c9b9362434b193df3f29a00e3c9c0c.zip\66802\江苏省2009届高三数学高考模拟试题精选(27套)\2009届江苏省东台中学高三第一学期期末数学考试试题.files\image329.gif) ,
,/file:///E:\cooco.net.cn\docfiles\down\test\down\e0c9b9362434b193df3f29a00e3c9c0c.zip\66802\江苏省2009届高三数学高考模拟试题精选(27套)\2009届江苏省东台中学高三第一学期期末数学考试试题.files\image331.gif) ,
,
∴平面/file:///E:\cooco.net.cn\docfiles\down\test\down\e0c9b9362434b193df3f29a00e3c9c0c.zip\66802\江苏省2009届高三数学高考模拟试题精选(27套)\2009届江苏省东台中学高三第一学期期末数学考试试题.files\image333.gif) 面
面/file:///E:\cooco.net.cn\docfiles\down\test\down\e0c9b9362434b193df3f29a00e3c9c0c.zip\66802\江苏省2009届高三数学高考模拟试题精选(27套)\2009届江苏省东台中学高三第一学期期末数学考试试题.files\image135.gif) . …………………………………9分
. …………………………………9分
又/file:///E:\cooco.net.cn\docfiles\down\test\down\e0c9b9362434b193df3f29a00e3c9c0c.zip\66802\江苏省2009届高三数学高考模拟试题精选(27套)\2009届江苏省东台中学高三第一学期期末数学考试试题.files\image336.gif) 平面
平面/file:///E:\cooco.net.cn\docfiles\down\test\down\e0c9b9362434b193df3f29a00e3c9c0c.zip\66802\江苏省2009届高三数学高考模拟试题精选(27套)\2009届江苏省东台中学高三第一学期期末数学考试试题.files\image338.gif) ,∴
,∴/file:///E:\cooco.net.cn\docfiles\down\test\down\e0c9b9362434b193df3f29a00e3c9c0c.zip\66802\江苏省2009届高三数学高考模拟试题精选(27套)\2009届江苏省东台中学高三第一学期期末数学考试试题.files\image133.gif) 面
面/file:///E:\cooco.net.cn\docfiles\down\test\down\e0c9b9362434b193df3f29a00e3c9c0c.zip\66802\江苏省2009届高三数学高考模拟试题精选(27套)\2009届江苏省东台中学高三第一学期期末数学考试试题.files\image135.gif) . ………………10分
. ………………10分
(Ⅲ)/file:///E:\cooco.net.cn\docfiles\down\test\down\e0c9b9362434b193df3f29a00e3c9c0c.zip\66802\江苏省2009届高三数学高考模拟试题精选(27套)\2009届江苏省东台中学高三第一学期期末数学考试试题.files\image341.gif) . ……………………………12分
. ……………………………12分
/file:///E:\cooco.net.cn\docfiles\down\test\down\e0c9b9362434b193df3f29a00e3c9c0c.zip\66802\江苏省2009届高三数学高考模拟试题精选(27套)\2009届江苏省东台中学高三第一学期期末数学考试试题.files\image343.gif) . ……………………………15分
. ……………………………15分
18.解: (1)由/file:///E:\cooco.net.cn\docfiles\down\test\down\e0c9b9362434b193df3f29a00e3c9c0c.zip\66802\江苏省2009届高三数学高考模拟试题精选(27套)\2009届江苏省东台中学高三第一学期期末数学考试试题.files\image139.gif) ,得
,得/file:///E:\cooco.net.cn\docfiles\down\test\down\e0c9b9362434b193df3f29a00e3c9c0c.zip\66802\江苏省2009届高三数学高考模拟试题精选(27套)\2009届江苏省东台中学高三第一学期期末数学考试试题.files\image346.gif) ,
,
则由/file:///E:\cooco.net.cn\docfiles\down\test\down\e0c9b9362434b193df3f29a00e3c9c0c.zip\66802\江苏省2009届高三数学高考模拟试题精选(27套)\2009届江苏省东台中学高三第一学期期末数学考试试题.files\image348.gif) ,解得F(3,0) 设椭圆
,解得F(3,0) 设椭圆/file:///E:\cooco.net.cn\docfiles\down\test\down\e0c9b9362434b193df3f29a00e3c9c0c.zip\66802\江苏省2009届高三数学高考模拟试题精选(27套)\2009届江苏省东台中学高三第一学期期末数学考试试题.files\image143.gif) 的方程为
的方程为/file:///E:\cooco.net.cn\docfiles\down\test\down\e0c9b9362434b193df3f29a00e3c9c0c.zip\66802\江苏省2009届高三数学高考模拟试题精选(27套)\2009届江苏省东台中学高三第一学期期末数学考试试题.files\image350.gif) ,则
,则/file:///E:\cooco.net.cn\docfiles\down\test\down\e0c9b9362434b193df3f29a00e3c9c0c.zip\66802\江苏省2009届高三数学高考模拟试题精选(27套)\2009届江苏省东台中学高三第一学期期末数学考试试题.files\image352.gif) ,解得
,解得/file:///E:\cooco.net.cn\docfiles\down\test\down\e0c9b9362434b193df3f29a00e3c9c0c.zip\66802\江苏省2009届高三数学高考模拟试题精选(27套)\2009届江苏省东台中学高三第一学期期末数学考试试题.files\image354.gif) 所以椭圆
所以椭圆/file:///E:\cooco.net.cn\docfiles\down\test\down\e0c9b9362434b193df3f29a00e3c9c0c.zip\66802\江苏省2009届高三数学高考模拟试题精选(27套)\2009届江苏省东台中学高三第一学期期末数学考试试题.files\image143.gif) 的方程为
的方程为/file:///E:\cooco.net.cn\docfiles\down\test\down\e0c9b9362434b193df3f29a00e3c9c0c.zip\66802\江苏省2009届高三数学高考模拟试题精选(27套)\2009届江苏省东台中学高三第一学期期末数学考试试题.files\image356.gif)
(2)因为点/file:///E:\cooco.net.cn\docfiles\down\test\down\e0c9b9362434b193df3f29a00e3c9c0c.zip\66802\江苏省2009届高三数学高考模拟试题精选(27套)\2009届江苏省东台中学高三第一学期期末数学考试试题.files\image150.gif) 在椭圆
在椭圆/file:///E:\cooco.net.cn\docfiles\down\test\down\e0c9b9362434b193df3f29a00e3c9c0c.zip\66802\江苏省2009届高三数学高考模拟试题精选(27套)\2009届江苏省东台中学高三第一学期期末数学考试试题.files\image143.gif) 上运动,所以
上运动,所以/file:///E:\cooco.net.cn\docfiles\down\test\down\e0c9b9362434b193df3f29a00e3c9c0c.zip\66802\江苏省2009届高三数学高考模拟试题精选(27套)\2009届江苏省东台中学高三第一学期期末数学考试试题.files\image358.gif) , 从而圆心
, 从而圆心/file:///E:\cooco.net.cn\docfiles\down\test\down\e0c9b9362434b193df3f29a00e3c9c0c.zip\66802\江苏省2009届高三数学高考模拟试题精选(27套)\2009届江苏省东台中学高三第一学期期末数学考试试题.files\image154.gif) 到直线
到直线/file:///E:\cooco.net.cn\docfiles\down\test\down\e0c9b9362434b193df3f29a00e3c9c0c.zip\66802\江苏省2009届高三数学高考模拟试题精选(27套)\2009届江苏省东台中学高三第一学期期末数学考试试题.files\image148.gif) 的距离
的距离/file:///E:\cooco.net.cn\docfiles\down\test\down\e0c9b9362434b193df3f29a00e3c9c0c.zip\66802\江苏省2009届高三数学高考模拟试题精选(27套)\2009届江苏省东台中学高三第一学期期末数学考试试题.files\image361.gif) . 所以直线
. 所以直线/file:///E:\cooco.net.cn\docfiles\down\test\down\e0c9b9362434b193df3f29a00e3c9c0c.zip\66802\江苏省2009届高三数学高考模拟试题精选(27套)\2009届江苏省东台中学高三第一学期期末数学考试试题.files\image152.gif) 与圆
与圆/file:///E:\cooco.net.cn\docfiles\down\test\down\e0c9b9362434b193df3f29a00e3c9c0c.zip\66802\江苏省2009届高三数学高考模拟试题精选(27套)\2009届江苏省东台中学高三第一学期期末数学考试试题.files\image154.gif) 恒相交
恒相交
又直线/file:///E:\cooco.net.cn\docfiles\down\test\down\e0c9b9362434b193df3f29a00e3c9c0c.zip\66802\江苏省2009届高三数学高考模拟试题精选(27套)\2009届江苏省东台中学高三第一学期期末数学考试试题.files\image152.gif) 被圆
被圆/file:///E:\cooco.net.cn\docfiles\down\test\down\e0c9b9362434b193df3f29a00e3c9c0c.zip\66802\江苏省2009届高三数学高考模拟试题精选(27套)\2009届江苏省东台中学高三第一学期期末数学考试试题.files\image154.gif) 截得的弦长为
截得的弦长为/file:///E:\cooco.net.cn\docfiles\down\test\down\e0c9b9362434b193df3f29a00e3c9c0c.zip\66802\江苏省2009届高三数学高考模拟试题精选(27套)\2009届江苏省东台中学高三第一学期期末数学考试试题.files\image363.gif)
/file:///E:\cooco.net.cn\docfiles\down\test\down\e0c9b9362434b193df3f29a00e3c9c0c.zip\66802\江苏省2009届高三数学高考模拟试题精选(27套)\2009届江苏省东台中学高三第一学期期末数学考试试题.files\image365.gif)
由于/file:///E:\cooco.net.cn\docfiles\down\test\down\e0c9b9362434b193df3f29a00e3c9c0c.zip\66802\江苏省2009届高三数学高考模拟试题精选(27套)\2009届江苏省东台中学高三第一学期期末数学考试试题.files\image367.gif) ,所以
,所以/file:///E:\cooco.net.cn\docfiles\down\test\down\e0c9b9362434b193df3f29a00e3c9c0c.zip\66802\江苏省2009届高三数学高考模拟试题精选(27套)\2009届江苏省东台中学高三第一学期期末数学考试试题.files\image369.gif) ,则
,则/file:///E:\cooco.net.cn\docfiles\down\test\down\e0c9b9362434b193df3f29a00e3c9c0c.zip\66802\江苏省2009届高三数学高考模拟试题精选(27套)\2009届江苏省东台中学高三第一学期期末数学考试试题.files\image371.gif) ,
,
即直线/file:///E:\cooco.net.cn\docfiles\down\test\down\e0c9b9362434b193df3f29a00e3c9c0c.zip\66802\江苏省2009届高三数学高考模拟试题精选(27套)\2009届江苏省东台中学高三第一学期期末数学考试试题.files\image152.gif) 被圆
被圆/file:///E:\cooco.net.cn\docfiles\down\test\down\e0c9b9362434b193df3f29a00e3c9c0c.zip\66802\江苏省2009届高三数学高考模拟试题精选(27套)\2009届江苏省东台中学高三第一学期期末数学考试试题.files\image154.gif) 截得的弦长的取值范围是
截得的弦长的取值范围是/file:///E:\cooco.net.cn\docfiles\down\test\down\e0c9b9362434b193df3f29a00e3c9c0c.zip\66802\江苏省2009届高三数学高考模拟试题精选(27套)\2009届江苏省东台中学高三第一学期期末数学考试试题.files\image371.gif)
19. 解:⑴g(t) 的值域为[0,/file:///E:\cooco.net.cn\docfiles\down\test\down\e0c9b9362434b193df3f29a00e3c9c0c.zip\66802\江苏省2009届高三数学高考模拟试题精选(27套)\2009届江苏省东台中学高三第一学期期末数学考试试题.files\image373.gif) ]…………………5分
]…………………5分
⑵
/file:///E:\cooco.net.cn\docfiles\down\test\down\e0c9b9362434b193df3f29a00e3c9c0c.zip\66802\江苏省2009届高三数学高考模拟试题精选(27套)\2009届江苏省东台中学高三第一学期期末数学考试试题.files\image375.gif) …………………10分
…………………10分
⑶当/file:///E:\cooco.net.cn\docfiles\down\test\down\e0c9b9362434b193df3f29a00e3c9c0c.zip\66802\江苏省2009届高三数学高考模拟试题精选(27套)\2009届江苏省东台中学高三第一学期期末数学考试试题.files\image377.gif) 时,
时,/file:///E:\cooco.net.cn\docfiles\down\test\down\e0c9b9362434b193df3f29a00e3c9c0c.zip\66802\江苏省2009届高三数学高考模拟试题精选(27套)\2009届江苏省东台中学高三第一学期期末数学考试试题.files\image379.gif)
/file:///E:\cooco.net.cn\docfiles\down\test\down\e0c9b9362434b193df3f29a00e3c9c0c.zip\66802\江苏省2009届高三数学高考模拟试题精选(27套)\2009届江苏省东台中学高三第一学期期末数学考试试题.files\image381.gif) ≤
≤/file:///E:\cooco.net.cn\docfiles\down\test\down\e0c9b9362434b193df3f29a00e3c9c0c.zip\66802\江苏省2009届高三数学高考模拟试题精选(27套)\2009届江苏省东台中学高三第一学期期末数学考试试题.files\image383.gif) +
+/file:///E:\cooco.net.cn\docfiles\down\test\down\e0c9b9362434b193df3f29a00e3c9c0c.zip\66802\江苏省2009届高三数学高考模拟试题精选(27套)\2009届江苏省东台中学高三第一学期期末数学考试试题.files\image385.gif) =
=/file:///E:\cooco.net.cn\docfiles\down\test\down\e0c9b9362434b193df3f29a00e3c9c0c.zip\66802\江苏省2009届高三数学高考模拟试题精选(27套)\2009届江苏省东台中学高三第一学期期末数学考试试题.files\image387.gif) <2;
<2;
当/file:///E:\cooco.net.cn\docfiles\down\test\down\e0c9b9362434b193df3f29a00e3c9c0c.zip\66802\江苏省2009届高三数学高考模拟试题精选(27套)\2009届江苏省东台中学高三第一学期期末数学考试试题.files\image389.gif) 时,
时,/file:///E:\cooco.net.cn\docfiles\down\test\down\e0c9b9362434b193df3f29a00e3c9c0c.zip\66802\江苏省2009届高三数学高考模拟试题精选(27套)\2009届江苏省东台中学高三第一学期期末数学考试试题.files\image379.gif)
/file:///E:\cooco.net.cn\docfiles\down\test\down\e0c9b9362434b193df3f29a00e3c9c0c.zip\66802\江苏省2009届高三数学高考模拟试题精选(27套)\2009届江苏省东台中学高三第一学期期末数学考试试题.files\image391.gif) ≤
≤/file:///E:\cooco.net.cn\docfiles\down\test\down\e0c9b9362434b193df3f29a00e3c9c0c.zip\66802\江苏省2009届高三数学高考模拟试题精选(27套)\2009届江苏省东台中学高三第一学期期末数学考试试题.files\image393.gif) .
.
所以若按给定的函数模型预测,该市目前的大气环境综合指数不会超标。…………………15分
20.解:(1)/file:///E:\cooco.net.cn\docfiles\down\test\down\e0c9b9362434b193df3f29a00e3c9c0c.zip\66802\江苏省2009届高三数学高考模拟试题精选(27套)\2009届江苏省东台中学高三第一学期期末数学考试试题.files\image395.gif)
当/file:///E:\cooco.net.cn\docfiles\down\test\down\e0c9b9362434b193df3f29a00e3c9c0c.zip\66802\江苏省2009届高三数学高考模拟试题精选(27套)\2009届江苏省东台中学高三第一学期期末数学考试试题.files\image397.gif) 时,
时,/file:///E:\cooco.net.cn\docfiles\down\test\down\e0c9b9362434b193df3f29a00e3c9c0c.zip\66802\江苏省2009届高三数学高考模拟试题精选(27套)\2009届江苏省东台中学高三第一学期期末数学考试试题.files\image399.gif) 时,
时,/file:///E:\cooco.net.cn\docfiles\down\test\down\e0c9b9362434b193df3f29a00e3c9c0c.zip\66802\江苏省2009届高三数学高考模拟试题精选(27套)\2009届江苏省东台中学高三第一学期期末数学考试试题.files\image401.gif) ,
,
/file:///E:\cooco.net.cn\docfiles\down\test\down\e0c9b9362434b193df3f29a00e3c9c0c.zip\66802\江苏省2009届高三数学高考模拟试题精选(27套)\2009届江苏省东台中学高三第一学期期末数学考试试题.files\image403.gif)
/file:///E:\cooco.net.cn\docfiles\down\test\down\e0c9b9362434b193df3f29a00e3c9c0c.zip\66802\江苏省2009届高三数学高考模拟试题精选(27套)\2009届江苏省东台中学高三第一学期期末数学考试试题.files\image405.gif) 的极小值是
的极小值是/file:///E:\cooco.net.cn\docfiles\down\test\down\e0c9b9362434b193df3f29a00e3c9c0c.zip\66802\江苏省2009届高三数学高考模拟试题精选(27套)\2009届江苏省东台中学高三第一学期期末数学考试试题.files\image407.gif)
(2)/file:///E:\cooco.net.cn\docfiles\down\test\down\e0c9b9362434b193df3f29a00e3c9c0c.zip\66802\江苏省2009届高三数学高考模拟试题精选(27套)\2009届江苏省东台中学高三第一学期期末数学考试试题.files\image409.gif) ,
,/file:///E:\cooco.net.cn\docfiles\down\test\down\e0c9b9362434b193df3f29a00e3c9c0c.zip\66802\江苏省2009届高三数学高考模拟试题精选(27套)\2009届江苏省东台中学高三第一学期期末数学考试试题.files\image411.gif) 要使直线
要使直线/file:///E:\cooco.net.cn\docfiles\down\test\down\e0c9b9362434b193df3f29a00e3c9c0c.zip\66802\江苏省2009届高三数学高考模拟试题精选(27套)\2009届江苏省东台中学高三第一学期期末数学考试试题.files\image168.gif) 对任意的
对任意的
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com