
题目列表(包括答案和解析)
| 5 |
| 4 | ||
|
| ||
| 2 |
| 5 |
| 4 | ||
|
| ||
| 2 |
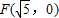 与定直线l:
与定直线l: 的距离之比是常数
的距离之比是常数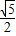 .
.已知平面内一动点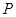 到点
到点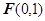 的距离与点
的距离与点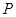 到
到 轴的距离的差等于1.(I)求动点
轴的距离的差等于1.(I)求动点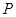 的轨迹
的轨迹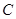 的方程;(II)过点
的方程;(II)过点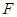 作两条斜率存在且互相垂直的直线
作两条斜率存在且互相垂直的直线 ,设
,设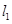 与轨迹
与轨迹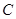 相交于点
相交于点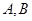 ,
, 与轨迹
与轨迹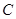 相交于点
相交于点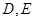 ,求
,求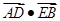 的最小值.
的最小值.
已知平面内一动点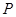 到点
到点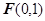 的距离与点
的距离与点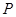 到
到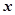 轴的距离的差等于1.(I)求动点
轴的距离的差等于1.(I)求动点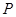 的轨迹
的轨迹 的方程;(II)过点
的方程;(II)过点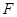 作两条斜率存在且互相垂直的直线
作两条斜率存在且互相垂直的直线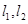 ,设
,设 与轨迹
与轨迹 相交于点
相交于点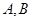 ,
,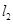 与轨迹
与轨迹 相交于点
相交于点 ,求
,求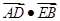 的最小值.
的最小值.
1./2009年江苏省大丰市高三年级调研考试数学试题.files/image206.gif) 2.
2. /2009年江苏省大丰市高三年级调研考试数学试题.files/image208.gif) 3. 6或14
4.36
5. 2
3. 6或14
4.36
5. 2
6.6,17,28,39,40,51,62,73 7.3 8./2009年江苏省大丰市高三年级调研考试数学试题.files/image210.gif)
9.点P(x1,x2)在圆/2009年江苏省大丰市高三年级调研考试数学试题.files/image038.gif) 内10.①②④11. 212.
内10.①②④11. 212./2009年江苏省大丰市高三年级调研考试数学试题.files/image212.gif)
13./2009年江苏省大丰市高三年级调研考试数学试题.files/image214.gif) 14.M=N
14.M=N
15. 解:(1)由/2009年江苏省大丰市高三年级调研考试数学试题.files/image216.gif) ,得
,得
/2009年江苏省大丰市高三年级调研考试数学试题.files/image218.gif) ,…………………………2分
,…………………………2分
/2009年江苏省大丰市高三年级调研考试数学试题.files/image220.gif) ,
,
/2009年江苏省大丰市高三年级调研考试数学试题.files/image222.gif) ,
, /2009年江苏省大丰市高三年级调研考试数学试题.files/image224.gif) ,
,
于是/2009年江苏省大丰市高三年级调研考试数学试题.files/image226.gif) ,
, /2009年江苏省大丰市高三年级调研考试数学试题.files/image228.gif) ,
,
∴/2009年江苏省大丰市高三年级调研考试数学试题.files/image230.gif) ,即
,即/2009年江苏省大丰市高三年级调研考试数学试题.files/image082.gif)
/2009年江苏省大丰市高三年级调研考试数学试题.files/image233.gif) .…………………………7分
.…………………………7分
(2)∵/2009年江苏省大丰市高三年级调研考试数学试题.files/image080.gif) 角是一个三角形的最小内角,∴0<
角是一个三角形的最小内角,∴0</2009年江苏省大丰市高三年级调研考试数学试题.files/image080.gif) ≤
≤/2009年江苏省大丰市高三年级调研考试数学试题.files/image236.gif) ,
,/2009年江苏省大丰市高三年级调研考试数学试题.files/image238.gif) ,………………10分
,………………10分
设/2009年江苏省大丰市高三年级调研考试数学试题.files/image240.gif) ,则
,则/2009年江苏省大丰市高三年级调研考试数学试题.files/image240.gif) ≥
≥/2009年江苏省大丰市高三年级调研考试数学试题.files/image243.gif) (当且仅当
(当且仅当/2009年江苏省大丰市高三年级调研考试数学试题.files/image245.gif) 时取=),………12分
时取=),………12分
故函数/2009年江苏省大丰市高三年级调研考试数学试题.files/image082.gif) 的值域为
的值域为/2009年江苏省大丰市高三年级调研考试数学试题.files/image247.gif) .………………………………14分
.………………………………14分
16.证明:(1)/2009年江苏省大丰市高三年级调研考试数学试题.files/image249.gif) 同理,
同理,/2009年江苏省大丰市高三年级调研考试数学试题.files/image251.gif)
又∵/2009年江苏省大丰市高三年级调研考试数学试题.files/image253.gif) ∴
∴/2009年江苏省大丰市高三年级调研考试数学试题.files/image255.gif) 平面
平面/2009年江苏省大丰市高三年级调研考试数学试题.files/image257.gif) . …………………5分
. …………………5分
(2)由(1)有/2009年江苏省大丰市高三年级调研考试数学试题.files/image255.gif) 平面
平面/2009年江苏省大丰市高三年级调研考试数学试题.files/image257.gif)
又∵/2009年江苏省大丰市高三年级调研考试数学试题.files/image259.gif) 平面
平面/2009年江苏省大丰市高三年级调研考试数学试题.files/image097.gif) , ∴平面
, ∴平面/2009年江苏省大丰市高三年级调研考试数学试题.files/image095.gif) 平面
平面/2009年江苏省大丰市高三年级调研考试数学试题.files/image097.gif) .………………9分
.………………9分
(3)连接AG并延长交CD于H,连接EH,则/2009年江苏省大丰市高三年级调研考试数学试题.files/image263.gif) ,
,
在AE上取点F使得/2009年江苏省大丰市高三年级调研考试数学试题.files/image265.gif) ,则
,则/2009年江苏省大丰市高三年级调研考试数学试题.files/image267.gif) ,易知GF
,易知GF/2009年江苏省大丰市高三年级调研考试数学试题.files/image101.gif) 平面CDE.…………………14分
平面CDE.…………………14分
17.解:(1)/2009年江苏省大丰市高三年级调研考试数学试题.files/image270.gif) ,
………3分
,
………3分
/2009年江苏省大丰市高三年级调研考试数学试题.files/image272.gif) ,
,/2009年江苏省大丰市高三年级调研考试数学试题.files/image274.gif) ,
………6分
,
………6分
∴/2009年江苏省大丰市高三年级调研考试数学试题.files/image276.gif) 。 ………8分
。 ………8分
(2)∵/2009年江苏省大丰市高三年级调研考试数学试题.files/image278.gif) ,……11分
,……11分
∴当且仅当/2009年江苏省大丰市高三年级调研考试数学试题.files/image280.gif) ,即
,即/2009年江苏省大丰市高三年级调研考试数学试题.files/image282.gif) 时,
时,/2009年江苏省大丰市高三年级调研考试数学试题.files/image111.gif) 有最大值。……13分
有最大值。……13分
∵/2009年江苏省大丰市高三年级调研考试数学试题.files/image284.gif) ,∴取
,∴取/2009年江苏省大丰市高三年级调研考试数学试题.files/image286.gif) 时,
时,/2009年江苏省大丰市高三年级调研考试数学试题.files/image288.gif) (元),
(元),
此时,/2009年江苏省大丰市高三年级调研考试数学试题.files/image290.gif) (元)。答:第3天或第17天销售收入最高,此时应将单价
(元)。答:第3天或第17天销售收入最高,此时应将单价/2009年江苏省大丰市高三年级调研考试数学试题.files/image103.gif) 定为7元为好
定为7元为好
18. 解:(1)设M/2009年江苏省大丰市高三年级调研考试数学试题.files/image292.gif)
∵点M在MA上∴/2009年江苏省大丰市高三年级调研考试数学试题.files/image294.gif) ①……………………3分
①……………………3分
同理可得/2009年江苏省大丰市高三年级调研考试数学试题.files/image296.gif) ②…………………………5分
②…………………………5分
由①②知AB的方程为/2009年江苏省大丰市高三年级调研考试数学试题.files/image298.gif) …………6分
…………6分
易知右焦点F(/2009年江苏省大丰市高三年级调研考试数学试题.files/image300.gif) )满足③式,故AB恒过椭圆C的右焦点F(
)满足③式,故AB恒过椭圆C的右焦点F(/2009年江苏省大丰市高三年级调研考试数学试题.files/image300.gif) )……8分
)……8分
(2)把AB的方程/2009年江苏省大丰市高三年级调研考试数学试题.files/image302.gif)
∴/2009年江苏省大丰市高三年级调研考试数学试题.files/image304.gif) ……………………12分
……………………12分
又M到AB的距离/2009年江苏省大丰市高三年级调研考试数学试题.files/image306.gif)
∴△ABM的面积/2009年江苏省大丰市高三年级调研考试数学试题.files/image308.gif) ……………………15分
……………………15分
19解:(Ⅰ) /2009年江苏省大丰市高三年级调研考试数学试题.files/image310.gif)
/2009年江苏省大丰市高三年级调研考试数学试题.files/image312.gif) …………………………
…………………………
所以函数/2009年江苏省大丰市高三年级调研考试数学试题.files/image058.gif) 在
在/2009年江苏省大丰市高三年级调研考试数学试题.files/image315.gif) 上是单调减函数.
上是单调减函数./2009年江苏省大丰市高三年级调研考试数学试题.files/image317.gif) …………………………4分
…………………………4分
(Ⅱ) 证明:据题意/2009年江苏省大丰市高三年级调研考试数学试题.files/image135.gif) 且x1<x2<x3,
且x1<x2<x3,
由(Ⅰ)知f
(x1)>f (x2)>f (x3), x2=/2009年江苏省大丰市高三年级调研考试数学试题.files/image319.gif) …………………………6分
…………………………6分
/2009年江苏省大丰市高三年级调研考试数学试题.files/image321.gif)
/2009年江苏省大丰市高三年级调研考试数学试题.files/image323.gif) …………………8分
…………………8分
/2009年江苏省大丰市高三年级调研考试数学试题.files/image325.gif)
/2009年江苏省大丰市高三年级调研考试数学试题.files/image327.gif)
即ㄓ/2009年江苏省大丰市高三年级调研考试数学试题.files/image097.gif) 是钝角三角形……………………………………..10分
是钝角三角形……………………………………..10分
(Ⅲ)/2009年江苏省大丰市高三年级调研考试数学试题.files/image329.gif) 假设ㄓ
假设ㄓ/2009年江苏省大丰市高三年级调研考试数学试题.files/image097.gif) 为等腰三角形,则只能是
为等腰三角形,则只能是/2009年江苏省大丰市高三年级调研考试数学试题.files/image332.gif)
/2009年江苏省大丰市高三年级调研考试数学试题.files/image334.gif) 即
即/2009年江苏省大丰市高三年级调研考试数学试题.files/image336.gif)
/2009年江苏省大丰市高三年级调研考试数学试题.files/image338.gif)
/2009年江苏省大丰市高三年级调研考试数学试题.files/image340.gif)
/2009年江苏省大丰市高三年级调研考试数学试题.files/image342.gif)
/2009年江苏省大丰市高三年级调研考试数学试题.files/image344.gif)
/2009年江苏省大丰市高三年级调研考试数学试题.files/image346.gif) ①
…………………………………………..14分
①
…………………………………………..14分
而事实上, /2009年江苏省大丰市高三年级调研考试数学试题.files/image348.gif) ②
②
由于/2009年江苏省大丰市高三年级调研考试数学试题.files/image350.gif) ,故(2)式等号不成立.这与
,故(2)式等号不成立.这与/2009年江苏省大丰市高三年级调研考试数学试题.files/image352.gif) 式矛盾. 所以ㄓ
式矛盾. 所以ㄓ/2009年江苏省大丰市高三年级调研考试数学试题.files/image097.gif) 不可能为等腰三角形..16分
不可能为等腰三角形..16分
20. [解]
(Ⅰ)/2009年江苏省大丰市高三年级调研考试数学试题.files/image355.gif)
/2009年江苏省大丰市高三年级调研考试数学试题.files/image357.gif) … 2分
… 2分
故数列/2009年江苏省大丰市高三年级调研考试数学试题.files/image147.gif) 为等比数列,公比为3. ……… 4分
为等比数列,公比为3. ……… 4分
(Ⅱ)/2009年江苏省大丰市高三年级调研考试数学试题.files/image359.gif)
/2009年江苏省大丰市高三年级调研考试数学试题.files/image361.gif) ……… 6分
……… 6分
所以数列/2009年江苏省大丰市高三年级调研考试数学试题.files/image363.gif) 是以
是以/2009年江苏省大丰市高三年级调研考试数学试题.files/image365.gif) 为首项,公差为 loga3的等差数列.
为首项,公差为 loga3的等差数列.
又/2009年江苏省大丰市高三年级调研考试数学试题.files/image367.gif)
/2009年江苏省大丰市高三年级调研考试数学试题.files/image369.gif) ……… 8分
……… 8分
又/2009年江苏省大丰市高三年级调研考试数学试题.files/image371.gif) =1+3
=1+3/2009年江苏省大丰市高三年级调研考试数学试题.files/image373.gif) ,且
,且/2009年江苏省大丰市高三年级调研考试数学试题.files/image161.gif)
/2009年江苏省大丰市高三年级调研考试数学试题.files/image376.gif)
/2009年江苏省大丰市高三年级调研考试数学试题.files/image378.gif) ……… 10分
……… 10分
(Ⅲ)/2009年江苏省大丰市高三年级调研考试数学试题.files/image380.gif)
/2009年江苏省大丰市高三年级调研考试数学试题.files/image382.gif)
/2009年江苏省大丰市高三年级调研考试数学试题.files/image384.gif)
假设第/2009年江苏省大丰市高三年级调研考试数学试题.files/image386.gif) 项后有
项后有/2009年江苏省大丰市高三年级调研考试数学试题.files/image167.gif)
/2009年江苏省大丰市高三年级调研考试数学试题.files/image389.gif) 即第
即第/2009年江苏省大丰市高三年级调研考试数学试题.files/image386.gif) 项后
项后/2009年江苏省大丰市高三年级调研考试数学试题.files/image391.gif) ,于是原命题等价于
,于是原命题等价于
/2009年江苏省大丰市高三年级调研考试数学试题.files/image393.gif)
/2009年江苏省大丰市高三年级调研考试数学试题.files/image395.gif) ……… 15分
……… 15分
/2009年江苏省大丰市高三年级调研考试数学试题.files/image397.gif) 故数列
故数列/2009年江苏省大丰市高三年级调研考试数学试题.files/image147.gif) 从
从/2009年江苏省大丰市高三年级调研考试数学试题.files/image399.gif) 项起满足
项起满足/2009年江苏省大丰市高三年级调研考试数学试题.files/image167.gif) . ……… 16分
. ……… 16分
附加题
1. 解:(Ⅰ)由条件得矩阵/2009年江苏省大丰市高三年级调研考试数学试题.files/image401.gif) ,
,
它的特征值为/2009年江苏省大丰市高三年级调研考试数学试题.files/image171.gif) 和
和/2009年江苏省大丰市高三年级调研考试数学试题.files/image173.gif) ,对应的特征向量为
,对应的特征向量为/2009年江苏省大丰市高三年级调研考试数学试题.files/image405.gif) 及
及/2009年江苏省大丰市高三年级调研考试数学试题.files/image407.gif) ;
;
(Ⅱ)/2009年江苏省大丰市高三年级调研考试数学试题.files/image409.gif) ,
,
椭圆/2009年江苏省大丰市高三年级调研考试数学试题.files/image177.gif) 在
在/2009年江苏省大丰市高三年级调研考试数学试题.files/image175.gif) 的作用下的新曲线的方程为
的作用下的新曲线的方程为/2009年江苏省大丰市高三年级调研考试数学试题.files/image411.gif) .
.
2. 已知A是曲线ρ=3cosθ上任意一点,求点A到直线ρcosθ=1距离的最大值和最小值。
将极坐标方程转化成直角坐标方程:
ρ=3cosθ即:x2+y2=3x,(x-/2009年江苏省大丰市高三年级调研考试数学试题.files/image413.gif) )2+y2=
)2+y2=/2009年江苏省大丰市高三年级调研考试数学试题.files/image415.gif)
ρcosθ=1即x=1直线与圆相交。
所求最大值为2,最小值为0
3. 解:(Ⅰ)ξ可能的取值为0,1,2,3.
P(ξ=0)=?==P(ξ=1)=?+?=P(ξ=2)=?+?=
P(ξ=3)=?=. ξ的分布列为
ξ
0
1
2
3
P
数学期望为Eξ=1.2.
(Ⅱ)所求的概率为
p=P(ξ≥2)=P(ξ=2)+P(ξ=3)=+=
4(解:(I)如图,取/2009年江苏省大丰市高三年级调研考试数学试题.files/image091.gif) 的中点
的中点/2009年江苏省大丰市高三年级调研考试数学试题.files/image089.gif) ,则
,则/2009年江苏省大丰市高三年级调研考试数学试题.files/image419.gif) ,因为
,因为/2009年江苏省大丰市高三年级调研考试数学试题.files/image421.gif) ,
,
/2009年江苏省大丰市高三年级调研考试数学试题.files/image423.jpg) 所以
所以/2009年江苏省大丰市高三年级调研考试数学试题.files/image425.gif) ,又
,又/2009年江苏省大丰市高三年级调研考试数学试题.files/image427.gif) 平面
平面/2009年江苏省大丰市高三年级调研考试数学试题.files/image097.gif) ,
,
以/2009年江苏省大丰市高三年级调研考试数学试题.files/image430.gif) 为
为/2009年江苏省大丰市高三年级调研考试数学试题.files/image432.gif) 轴建立空间坐标系,
轴建立空间坐标系,
则/2009年江苏省大丰市高三年级调研考试数学试题.files/image434.gif) ,
,/2009年江苏省大丰市高三年级调研考试数学试题.files/image436.gif) ,
,/2009年江苏省大丰市高三年级调研考试数学试题.files/image438.gif) ,
,
/2009年江苏省大丰市高三年级调研考试数学试题.files/image440.gif) ,
,/2009年江苏省大丰市高三年级调研考试数学试题.files/image442.gif) ,
,
/2009年江苏省大丰市高三年级调研考试数学试题.files/image444.gif) ,
,/2009年江苏省大丰市高三年级调研考试数学试题.files/image446.gif) ,
,
/2009年江苏省大丰市高三年级调研考试数学试题.files/image448.gif) ,由
,由/2009年江苏省大丰市高三年级调研考试数学试题.files/image450.gif) ,知
,知/2009年江苏省大丰市高三年级调研考试数学试题.files/image452.gif) ,
,
又/2009年江苏省大丰市高三年级调研考试数学试题.files/image194.gif) ,从而
,从而/2009年江苏省大丰市高三年级调研考试数学试题.files/image196.gif) 平面
平面/2009年江苏省大丰市高三年级调研考试数学试题.files/image198.gif) ;
;
(II)由/2009年江苏省大丰市高三年级调研考试数学试题.files/image454.gif)
/2009年江苏省大丰市高三年级调研考试数学试题.files/image456.gif) ,得
,得/2009年江苏省大丰市高三年级调研考试数学试题.files/image458.gif) 。
。
设平面/2009年江苏省大丰市高三年级调研考试数学试题.files/image202.gif) 的法向量为
的法向量为/2009年江苏省大丰市高三年级调研考试数学试题.files/image461.gif) ,
,/2009年江苏省大丰市高三年级调研考试数学试题.files/image463.gif) ,
,/2009年江苏省大丰市高三年级调研考试数学试题.files/image465.gif) ,所以
,所以
/2009年江苏省大丰市高三年级调研考试数学试题.files/image467.gif) ,设
,设/2009年江苏省大丰市高三年级调研考试数学试题.files/image469.gif) ,则
,则/2009年江苏省大丰市高三年级调研考试数学试题.files/image471.gif)
所以点/2009年江苏省大丰市高三年级调研考试数学试题.files/image473.gif) 到平面
到平面/2009年江苏省大丰市高三年级调研考试数学试题.files/image202.gif) 的距离
的距离/2009年江苏省大丰市高三年级调研考试数学试题.files/image475.gif)
/2009年江苏省大丰市高三年级调研考试数学试题.files/image477.gif) 。
。
(III)再设平面/2009年江苏省大丰市高三年级调研考试数学试题.files/image198.gif) 的法向量为
的法向量为/2009年江苏省大丰市高三年级调研考试数学试题.files/image480.gif) ,
,/2009年江苏省大丰市高三年级调研考试数学试题.files/image482.gif) ,
,/2009年江苏省大丰市高三年级调研考试数学试题.files/image448.gif) ,
,
所以
/2009年江苏省大丰市高三年级调研考试数学试题.files/image485.gif) ,设
,设/2009年江苏省大丰市高三年级调研考试数学试题.files/image469.gif) ,则
,则/2009年江苏省大丰市高三年级调研考试数学试题.files/image487.gif) ,
,
故/2009年江苏省大丰市高三年级调研考试数学试题.files/image489.gif)
/2009年江苏省大丰市高三年级调研考试数学试题.files/image491.gif) ,根据法向量的方向,
,根据法向量的方向,
可知二面角/2009年江苏省大丰市高三年级调研考试数学试题.files/image204.gif) 的余弦值大小为
的余弦值大小为/2009年江苏省大丰市高三年级调研考试数学试题.files/image493.gif)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com