
题目列表(包括答案和解析)
()(本小题满分12分)
如图,四棱锥S-ABCD 的底面是正方形,每条侧棱的长都是地面边长的![]() 倍,P为侧棱SD上的点。
倍,P为侧棱SD上的点。 
(Ⅰ)求证:AC⊥SD;
(Ⅱ)若SD⊥平面PAC,求二面角P-AC-D的大小
(Ⅲ)在(Ⅱ)的条件下,侧棱SC上是否存在一点E,使得BE∥平面PAC。若存在,求SE:EC的值;若不存在,试说明理由。
| x2 |
| a2 |
| y2 |
| 2 |
| ||
| 2 |
| ||
| 2 |
| OP |
| OM |
| ON |
| 1 |
| 2 |
| x | 2 0 |
| y | 2 0 |
已知函数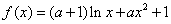 .
.
(Ⅰ)讨论函数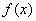 的单调性;
的单调性;
(Ⅱ)设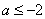 ,证明:对任意
,证明:对任意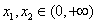 ,
,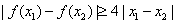 .
.
 1.选修4-1:几何证明选讲
1.选修4-1:几何证明选讲
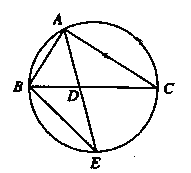
如图, 的角平分线
的角平分线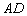 的延长线交它的外接圆于点
的延长线交它的外接圆于点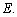
(Ⅰ)证明: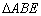 ∽△
∽△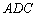 ;
;
(Ⅱ)若 的面积
的面积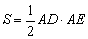 ,求
,求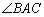 的大小.
的大小.
证明:(Ⅰ)由已知条件,可得∠BAE=∠CAD.
因为∠AEB与∠ACB是同弧上的圆周角,所以∠AEB=∠ACD.
故△ABE∽△ADC.
(Ⅱ)因为△ABE∽△ADC,所以 ,即AB·AC=AD·AE.
,即AB·AC=AD·AE.
又S= AB·ACsin∠BAC,且S=
AB·ACsin∠BAC,且S= AD·AE,故AB·ACsin∠BAC=AD·AE.
AD·AE,故AB·ACsin∠BAC=AD·AE.
则sin∠BAC=1,又∠BAC为三角形内角,所以∠BAC=90°.
已知函数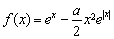 .
.
(Ⅰ)若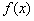 是
是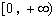 上是增函数,求实数a的取值范围;
上是增函数,求实数a的取值范围;
(Ⅱ)证明:当a≥1时,证明不等式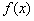 ≤x+1对x∈R恒成立;
≤x+1对x∈R恒成立;
(Ⅲ)对于在(0,1)中的任一个常数a,试探究是否存在x0>0,使得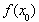 >x0+1成立?如果存在,请求出符合条件的一个x0;如果不存在,请说明理由.
>x0+1成立?如果存在,请求出符合条件的一个x0;如果不存在,请说明理由.
已知函数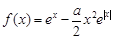 .
.
(Ⅰ)若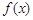 是
是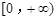 上是增函数,求实数a的取值范围;
上是增函数,求实数a的取值范围;
(Ⅱ)证明:当a≥1时,证明不等式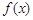 ≤x+1对x∈R恒成立;
≤x+1对x∈R恒成立;
(Ⅲ)对于在(0,1)中的任一个常数a,试探究是否存在x0>0,使得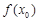 >x0+1成立?如果存在,请求出符合条件的一个x0;如果不存在,请说明理由.
>x0+1成立?如果存在,请求出符合条件的一个x0;如果不存在,请说明理由.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com