
题目列表(包括答案和解析)
命题“若![]() ,
,![]()
![]() ,
,![]()
![]() ,则
,则![]()
![]() .”可以如下证明:构造函数
.”可以如下证明:构造函数![]() ,则
,则![]() ,因为对一切
,因为对一切![]() ,恒有
,恒有![]() ,所以
,所以![]() ,故得
,故得![]()
![]() .
.
试解决下列问题:
(1)若![]() ,
,![]() ,
,![]()
![]() ,
,![]()
![]() ,求证
,求证![]()
![]() ;
;
(2)试将上述命题推广到n个实数,并证明你的结论.
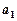 ,
,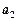
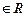 ,
,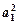
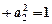 ,则
,则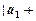
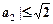 .”可以如下证明:构造函数
.”可以如下证明:构造函数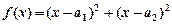 ,则
,则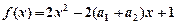 ,因为对一切
,因为对一切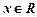 ,恒有
,恒有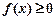 ,所以
,所以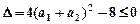 ,故得
,故得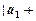
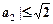 .
.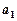 ,
,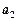 ,
,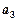
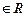 ,
,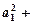
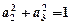 ,求证
,求证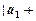
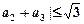 ;
;| 7 |
| 3 |
| 6 |
| 2 |
| 7 |
| 3 |
| 6 |
| 2 |
| 7 |
| 2 |
| 6 |
| 3 |
| 7 |
| 2 |
| 6 |
| 3 |
| 7 |
| 2 |
| 6 |
| 3 |
| 7 |
| 2 |
| 6 |
| 3 |
| 14 |
| 18 |
| 14 |
| 18 |
| 7 |
| 2 |
| 6 |
| 3 |
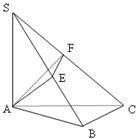
如图 ⊥平面
⊥平面 ,
,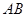 ⊥
⊥ ,过
,过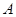 做
做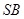
的垂线,垂足为 ,过
,过 做
做 的垂线,垂足为
的垂线,垂足为
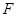 ,求证
,求证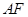 ⊥
⊥ 。以下是证明过程:
。以下是证明过程:
要证
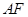 ⊥
⊥
只需证  ⊥平面
⊥平面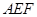
只需证 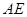 ⊥
⊥ (因为
(因为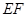 ⊥
⊥ )
)
只需证 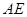 ⊥平面
⊥平面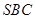
只需证 ① (因为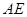 ⊥
⊥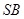 )
)
只需证  ⊥平面
⊥平面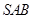
只需证 ② (因为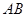 ⊥
⊥ )
)
由只需证 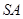 ⊥平面
⊥平面 可知上式成立
可知上式成立
所以 ⊥
⊥
把证明过程补充完整① ②
证明:假设___________,则∠B是直角或钝角.
(1)当∠B是直角时,因为∠C是直角,所以∠B+∠C=180°,与三角形的内角和定理矛盾.
(2)当∠B为钝角时,∠B+∠C>180°,同理矛盾.故___________,原命题成立.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com