
题目列表(包括答案和解析)
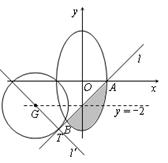
(本小题满分16分)已知椭圆![]() 的离心率为
的离心率为![]() ,过右顶点A的直线l与椭圆C相交于A、B两点,且
,过右顶点A的直线l与椭圆C相交于A、B两点,且![]() .
.
(1)求椭圆C和直线l的方程;
(2)记曲线C在直线l下方的部分与线段AB所围成的平面区域(含边界)为D.若曲线![]() 与D有公共点,试求实数m的最小值.
与D有公共点,试求实数m的最小值.
(本小题满分16分)
已知函数 =
=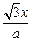 +
+ ,a≠0且a≠1.
,a≠0且a≠1.
(1)试就实数a的不同取值,写出该函数的单调增区间;
(2)已知当x>0时,函数在(0, )上单调递减,在(
)上单调递减,在( ,
,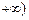 上单调递增,求a的值并写出函数的解析式;
上单调递增,求a的值并写出函数的解析式;
(3)记(2)中的函数图象为曲线C,试问是否存在经过原点的直线l,使得l为曲线C的对称轴?若存在,求出直线l的方程;若不存在,请说明理由.
(本小题满分16分)
已知圆C过点P(1,1),且与圆M: +
+ =
= (r>0)关于直线x+y+2=0对称.
(r>0)关于直线x+y+2=0对称.
(1)求圆C的方程;
(2)直线l过点Q(1,0.5),截圆C所得的弦长为2,求直线l的方程;
(3)过点P作两条相异直线分别与圆C相交于A,B,且直线PA和直线PB的倾斜角互补,O为坐标原点,试判断直线OP和AB是否平行?请说明理由.
(本小题满分16分)
已知椭圆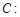
 的离心率为
的离心率为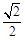 ,一条准线
,一条准线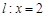 .
.
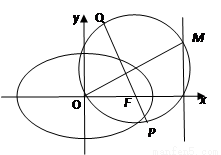
(1)求椭圆 的方程;
的方程;
(2)设O为坐标原点, 是
是 上的点,
上的点, 为椭圆
为椭圆 的右焦点,过点F作OM的垂线与以OM为直径的圆
的右焦点,过点F作OM的垂线与以OM为直径的圆 交于
交于 两点.
两点.
①若 ,求圆
,求圆 的方程;
的方程;
②若 是l上的动点,求证:点
是l上的动点,求证:点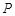 在定圆上,并求该定圆的方程.
在定圆上,并求该定圆的方程.
(本小题满分16分)
已知椭圆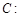
 的离心率为
的离心率为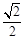 ,一条准线
,一条准线 .
.
(1)求椭圆 的方程;
的方程;
(2)设O为坐标原点,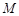 是
是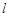 上的点,
上的点, 为椭圆
为椭圆 的右焦点,过点F作OM的垂线与以OM为直径的圆
的右焦点,过点F作OM的垂线与以OM为直径的圆 交于
交于 两点.
两点.
①若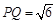 ,求圆
,求圆 的方程;
的方程;
②若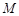 是l上的动点,求证点
是l上的动点,求证点 在定圆上,并求该定圆的方程.
在定圆上,并求该定圆的方程.
一、填空题:(每小题5分,共70分)
1.2 2. 1+2i 3.π 4. 9 5.充分不必要
6.(s,t) 7./江苏省高邮中学2009届高三第一学期期末数学试卷.files/image198.gif) 8.
8./江苏省高邮中学2009届高三第一学期期末数学试卷.files/image200.gif) 9.
9. /江苏省高邮中学2009届高三第一学期期末数学试卷.files/image202.gif) 10.
10./江苏省高邮中学2009届高三第一学期期末数学试卷.files/image204.gif)
11. /江苏省高邮中学2009届高三第一学期期末数学试卷.files/image206.gif) 12. 4 13.
12. 4 13./江苏省高邮中学2009届高三第一学期期末数学试卷.files/image208.gif) 14①③④
14①③④
二、解答题:(共90分)
15、(本小题满分14分)
解: (Ⅰ)因为各组的频率和等于1,故低于50分的频率为:
/江苏省高邮中学2009届高三第一学期期末数学试卷.files/image210.gif) ………………………………3分
………………………………3分
所以低于50分的人数为/江苏省高邮中学2009届高三第一学期期末数学试卷.files/image212.gif) (人)………………………………………….5分
(人)………………………………………….5分
(Ⅱ)依题意,成绩60及以上的分数所在的第三、四、五、六组(低于50分的为第一组),
频率和为 /江苏省高邮中学2009届高三第一学期期末数学试卷.files/image214.gif)
所以,抽样学生成绩的合格率是/江苏省高邮中学2009届高三第一学期期末数学试卷.files/image216.gif) %……………………………………………………8分.
%……………………………………………………8分.
于是,可以估计这次考试物理学科及格率约为/江苏省高邮中学2009届高三第一学期期末数学试卷.files/image216.gif) %……………………………………9分.
%……………………………………9分.
(Ⅲ)“成绩低于50分”及“[50,60)”的人数分别是6,9。所以从成绩不及格的学生中选两人,他们成绩至少有一个不低于50分的概率为:
/江苏省高邮中学2009届高三第一学期期末数学试卷.files/image218.gif) ……………………………………………………14分
……………………………………………………14分
16.(本小题满分14分)
解:/江苏省高邮中学2009届高三第一学期期末数学试卷.files/image220.gif)
(Ⅰ)当/江苏省高邮中学2009届高三第一学期期末数学试卷.files/image089.gif) 时,
时,/江苏省高邮中学2009届高三第一学期期末数学试卷.files/image222.gif) ………………………………3分
………………………………3分
/江苏省高邮中学2009届高三第一学期期末数学试卷.files/image224.gif) 当
当/江苏省高邮中学2009届高三第一学期期末数学试卷.files/image226.gif) 时,
时,/江苏省高邮中学2009届高三第一学期期末数学试卷.files/image091.gif) 是增函数,
是增函数,
所以函数/江苏省高邮中学2009届高三第一学期期末数学试卷.files/image091.gif) 的单调递增区间为
的单调递增区间为/江苏省高邮中学2009届高三第一学期期末数学试卷.files/image228.gif) . ……………7分
. ……………7分
(Ⅱ)由/江苏省高邮中学2009届高三第一学期期末数学试卷.files/image230.gif) 得
得/江苏省高邮中学2009届高三第一学期期末数学试卷.files/image232.gif) ,
, /江苏省高邮中学2009届高三第一学期期末数学试卷.files/image234.gif)
因为/江苏省高邮中学2009届高三第一学期期末数学试卷.files/image093.gif) ,所以当
,所以当/江苏省高邮中学2009届高三第一学期期末数学试卷.files/image236.gif) 时,
时,/江苏省高邮中学2009届高三第一学期期末数学试卷.files/image091.gif) 取最小值3,即
取最小值3,即/江苏省高邮中学2009届高三第一学期期末数学试卷.files/image238.gif)
当/江苏省高邮中学2009届高三第一学期期末数学试卷.files/image240.gif) 时,
时,/江苏省高邮中学2009届高三第一学期期末数学试卷.files/image091.gif) 取最大值4,即
取最大值4,即/江苏省高邮中学2009届高三第一学期期末数学试卷.files/image242.gif)
将/江苏省高邮中学2009届高三第一学期期末数学试卷.files/image242.gif) 代入(1)式得
代入(1)式得/江苏省高邮中学2009届高三第一学期期末数学试卷.files/image245.gif) . ………………………………14分
. ………………………………14分
/江苏省高邮中学2009届高三第一学期期末数学试卷.files/image253.gif)
17.(本小题满分14分)
(Ⅰ)证明:/江苏省高邮中学2009届高三第一学期期末数学试卷.files/image255.gif) 侧面
侧面/江苏省高邮中学2009届高三第一学期期末数学试卷.files/image257.gif) ,
,
/江苏省高邮中学2009届高三第一学期期末数学试卷.files/image259.gif) 侧面
侧面/江苏省高邮中学2009届高三第一学期期末数学试卷.files/image257.gif) ,
,/江苏省高邮中学2009届高三第一学期期末数学试卷.files/image262.gif) ,
,
………3分
在/江苏省高邮中学2009届高三第一学期期末数学试卷.files/image264.gif) 中,
中,/江苏省高邮中学2009届高三第一学期期末数学试卷.files/image266.gif) ,
,
则有/江苏省高邮中学2009届高三第一学期期末数学试卷.files/image268.gif) ,
,
/江苏省高邮中学2009届高三第一学期期末数学试卷.files/image270.gif) ,
,/江苏省高邮中学2009届高三第一学期期末数学试卷.files/image272.gif) ,
………………………………………6分
,
………………………………………6分
又/江苏省高邮中学2009届高三第一学期期末数学试卷.files/image274.gif)
/江苏省高邮中学2009届高三第一学期期末数学试卷.files/image276.gif) 平面
平面/江苏省高邮中学2009届高三第一学期期末数学试卷.files/image133.gif) . ……………………………………7分
. ……………………………………7分
(Ⅱ)证明:连/江苏省高邮中学2009届高三第一学期期末数学试卷.files/image279.gif) 、
、/江苏省高邮中学2009届高三第一学期期末数学试卷.files/image281.gif) ,连
,连/江苏省高邮中学2009届高三第一学期期末数学试卷.files/image283.gif) 交
交/江苏省高邮中学2009届高三第一学期期末数学试卷.files/image285.gif) 于
于/江苏省高邮中学2009届高三第一学期期末数学试卷.files/image019.gif) ,
,
/江苏省高邮中学2009届高三第一学期期末数学试卷.files/image288.gif) ,
,/江苏省高邮中学2009届高三第一学期期末数学试卷.files/image290.gif) ,
,/江苏省高邮中学2009届高三第一学期期末数学试卷.files/image292.gif) 四边形
四边形/江苏省高邮中学2009届高三第一学期期末数学试卷.files/image294.gif) 是平行四边形,……………10分
是平行四边形,……………10分
/江苏省高邮中学2009届高三第一学期期末数学试卷.files/image296.gif) ………………………11分
………………………11分
又/江苏省高邮中学2009届高三第一学期期末数学试卷.files/image298.gif) 平面
平面/江苏省高邮中学2009届高三第一学期期末数学试卷.files/image133.gif) ,
,/江苏省高邮中学2009届高三第一学期期末数学试卷.files/image301.gif) 平面
平面/江苏省高邮中学2009届高三第一学期期末数学试卷.files/image133.gif) ,
,
/江苏省高邮中学2009届高三第一学期期末数学试卷.files/image304.gif) 平面
平面/江苏省高邮中学2009届高三第一学期期末数学试卷.files/image133.gif) .
………………………14分
.
………………………14分
18.(本小题满分16分)
解:(I)/江苏省高邮中学2009届高三第一学期期末数学试卷.files/image307.gif) 为圆周的
为圆周的/江苏省高邮中学2009届高三第一学期期末数学试卷.files/image309.gif)
/江苏省高邮中学2009届高三第一学期期末数学试卷.files/image311.gif) 点到直线
点到直线/江苏省高邮中学2009届高三第一学期期末数学试卷.files/image141.gif) 的距离为
的距离为/江苏省高邮中学2009届高三第一学期期末数学试卷.files/image314.gif)
设/江苏省高邮中学2009届高三第一学期期末数学试卷.files/image141.gif) 的方程为
的方程为/江苏省高邮中学2009届高三第一学期期末数学试卷.files/image316.gif)
/江苏省高邮中学2009届高三第一学期期末数学试卷.files/image318.gif) 的方程为
的方程为/江苏省高邮中学2009届高三第一学期期末数学试卷.files/image320.gif) …5分
…5分
(II)设椭圆方程为/江苏省高邮中学2009届高三第一学期期末数学试卷.files/image322.gif) ,半焦距为c,则
,半焦距为c,则/江苏省高邮中学2009届高三第一学期期末数学试卷.files/image324.gif)
/江苏省高邮中学2009届高三第一学期期末数学试卷.files/image326.gif) 椭圆与圆O恰有两个不同的公共点,则
椭圆与圆O恰有两个不同的公共点,则/江苏省高邮中学2009届高三第一学期期末数学试卷.files/image328.gif) 或
或/江苏省高邮中学2009届高三第一学期期末数学试卷.files/image330.gif) ………………………………7分
………………………………7分
当/江苏省高邮中学2009届高三第一学期期末数学试卷.files/image328.gif) 时,
时,/江苏省高邮中学2009届高三第一学期期末数学试卷.files/image333.gif) 所求椭圆方程为
所求椭圆方程为/江苏省高邮中学2009届高三第一学期期末数学试卷.files/image335.gif) ;当
;当/江苏省高邮中学2009届高三第一学期期末数学试卷.files/image337.gif) 时,
时,/江苏省高邮中学2009届高三第一学期期末数学试卷.files/image339.gif)
/江苏省高邮中学2009届高三第一学期期末数学试卷.files/image341.gif) 所求椭圆方程为
所求椭圆方程为/江苏省高邮中学2009届高三第一学期期末数学试卷.files/image343.gif) ………………………………11分
………………………………11分
(III)设切点为N,则由题意得,在/江苏省高邮中学2009届高三第一学期期末数学试卷.files/image345.gif) 中,
中,/江苏省高邮中学2009届高三第一学期期末数学试卷.files/image347.gif) ,则
,则/江苏省高邮中学2009届高三第一学期期末数学试卷.files/image349.gif) ,
,
/江苏省高邮中学2009届高三第一学期期末数学试卷.files/image350.gif) N点的坐标为
N点的坐标为/江苏省高邮中学2009届高三第一学期期末数学试卷.files/image352.gif) ,……………………12分
,……………………12分
若椭圆为/江苏省高邮中学2009届高三第一学期期末数学试卷.files/image343.gif) 其焦点F1,F2
其焦点F1,F2
分别为点A,B故/江苏省高邮中学2009届高三第一学期期末数学试卷.files/image354.gif) ,
,
若椭圆为/江苏省高邮中学2009届高三第一学期期末数学试卷.files/image335.gif) ,其焦点为
,其焦点为/江苏省高邮中学2009届高三第一学期期末数学试卷.files/image356.gif) ,
,
此时/江苏省高邮中学2009届高三第一学期期末数学试卷.files/image358.gif) ………………………………16分
………………………………16分
19.(本小题满分16分)
解:(1)/江苏省高邮中学2009届高三第一学期期末数学试卷.files/image154.gif) 为等差数列,∵
为等差数列,∵/江苏省高邮中学2009届高三第一学期期末数学试卷.files/image361.gif) ,又
,又/江苏省高邮中学2009届高三第一学期期末数学试卷.files/image363.gif) ,
,
∴ /江苏省高邮中学2009届高三第一学期期末数学试卷.files/image365.gif) ,
,/江苏省高邮中学2009届高三第一学期期末数学试卷.files/image367.gif) 是方程
是方程/江苏省高邮中学2009届高三第一学期期末数学试卷.files/image369.gif) 的两个根
的两个根
又公差/江苏省高邮中学2009届高三第一学期期末数学试卷.files/image371.gif) ,∴
,∴/江苏省高邮中学2009届高三第一学期期末数学试卷.files/image373.gif) ,∴
,∴/江苏省高邮中学2009届高三第一学期期末数学试卷.files/image375.gif) ,
,/江苏省高邮中学2009届高三第一学期期末数学试卷.files/image377.gif) …………………………… 2分
…………………………… 2分
∴ /江苏省高邮中学2009届高三第一学期期末数学试卷.files/image379.gif) ∴
∴/江苏省高邮中学2009届高三第一学期期末数学试卷.files/image381.gif) ∴
∴/江苏省高邮中学2009届高三第一学期期末数学试卷.files/image383.gif) ……………………………… 4分
……………………………… 4分
(2)由(1)知,/江苏省高邮中学2009届高三第一学期期末数学试卷.files/image385.gif) ………………………………… 5分
………………………………… 5分
∴/江苏省高邮中学2009届高三第一学期期末数学试卷.files/image387.gif)
∴/江苏省高邮中学2009届高三第一学期期末数学试卷.files/image389.gif) ,
,/江苏省高邮中学2009届高三第一学期期末数学试卷.files/image391.gif) ,
,/江苏省高邮中学2009届高三第一学期期末数学试卷.files/image393.gif) ………………………………………… 7分
………………………………………… 7分
∵/江苏省高邮中学2009届高三第一学期期末数学试卷.files/image162.gif) 是等差数列,∴
是等差数列,∴/江苏省高邮中学2009届高三第一学期期末数学试卷.files/image396.gif) ,∴
,∴/江苏省高邮中学2009届高三第一学期期末数学试卷.files/image398.gif) ………………………… 8分
………………………… 8分
∴/江苏省高邮中学2009届高三第一学期期末数学试卷.files/image400.gif) (
(/江苏省高邮中学2009届高三第一学期期末数学试卷.files/image402.gif) 舍去) ……………………………………………………… 9分
舍去) ……………………………………………………… 9分
(3)由(2)得/江苏省高邮中学2009届高三第一学期期末数学试卷.files/image404.gif) …………………………………………………… 11分
…………………………………………………… 11分
/江苏省高邮中学2009届高三第一学期期末数学试卷.files/image406.gif) ,
,/江苏省高邮中学2009届高三第一学期期末数学试卷.files/image408.gif) 时取等号 … 13分
时取等号 … 13分
/江苏省高邮中学2009届高三第一学期期末数学试卷.files/image410.gif) ,
,/江苏省高邮中学2009届高三第一学期期末数学试卷.files/image412.gif) 时取等号15分
时取等号15分
(1)、(2)式中等号不可能同时取到,所以/江苏省高邮中学2009届高三第一学期期末数学试卷.files/image168.gif) ………………… 16分
………………… 16分
20. (本小题满分16分)
解(I)由题意:/江苏省高邮中学2009届高三第一学期期末数学试卷.files/image415.gif)
/江苏省高邮中学2009届高三第一学期期末数学试卷.files/image417.gif) ∴a=2
…………………………………………… 2分
∴a=2
…………………………………………… 2分
而/江苏省高邮中学2009届高三第一学期期末数学试卷.files/image419.gif) 所以h(x)在
所以h(x)在/江苏省高邮中学2009届高三第一学期期末数学试卷.files/image421.gif) 上为增函数,
上为增函数,/江苏省高邮中学2009届高三第一学期期末数学试卷.files/image423.gif) h(x)在
h(x)在/江苏省高邮中学2009届高三第一学期期末数学试卷.files/image425.gif) 上为增函数。………… 4分
上为增函数。………… 4分
(II)/江苏省高邮中学2009届高三第一学期期末数学试卷.files/image427.gif)
欲证:/江苏省高邮中学2009届高三第一学期期末数学试卷.files/image429.gif) 只需证:
只需证:/江苏省高邮中学2009届高三第一学期期末数学试卷.files/image431.gif) ,即证:
,即证:/江苏省高邮中学2009届高三第一学期期末数学试卷.files/image433.gif)
记/江苏省高邮中学2009届高三第一学期期末数学试卷.files/image435.gif)
∴/江苏省高邮中学2009届高三第一学期期末数学试卷.files/image437.gif)
∴当x>1时,/江苏省高邮中学2009届高三第一学期期末数学试卷.files/image439.gif) 为增函数……………………………….9分
为增函数……………………………….9分
/江苏省高邮中学2009届高三第一学期期末数学试卷.files/image441.gif)
即/江苏省高邮中学2009届高三第一学期期末数学试卷.files/image443.gif)
∴结论成立 ………………………………………………………………10分
(III)由 (1)知:/江苏省高邮中学2009届高三第一学期期末数学试卷.files/image445.gif)
∴/江苏省高邮中学2009届高三第一学期期末数学试卷.files/image180.gif) 对应表达式为
对应表达式为/江苏省高邮中学2009届高三第一学期期末数学试卷.files/image448.gif)
∴问题转化成求函数/江苏省高邮中学2009届高三第一学期期末数学试卷.files/image450.gif)
即求方程:/江苏省高邮中学2009届高三第一学期期末数学试卷.files/image452.gif)
即:/江苏省高邮中学2009届高三第一学期期末数学试卷.files/image454.gif)
设/江苏省高邮中学2009届高三第一学期期末数学试卷.files/image456.gif)
/江苏省高邮中学2009届高三第一学期期末数学试卷.files/image458.gif)
/江苏省高邮中学2009届高三第一学期期末数学试卷.files/image460.jpg) ∴当
∴当/江苏省高邮中学2009届高三第一学期期末数学试卷.files/image462.gif) 时,
时,/江苏省高邮中学2009届高三第一学期期末数学试卷.files/image464.gif) 为减函数.
为减函数.
当/江苏省高邮中学2009届高三第一学期期末数学试卷.files/image466.gif) 时,
时,/江苏省高邮中学2009届高三第一学期期末数学试卷.files/image468.gif) 为增函数.
为增函数.
而/江苏省高邮中学2009届高三第一学期期末数学试卷.files/image470.gif) 的图象开口向下的抛物线
的图象开口向下的抛物线
∴/江苏省高邮中学2009届高三第一学期期末数学试卷.files/image472.gif) 与
与/江苏省高邮中学2009届高三第一学期期末数学试卷.files/image474.gif) 的大致图象如图:
的大致图象如图:
∴/江苏省高邮中学2009届高三第一学期期末数学试卷.files/image472.gif) 与
与/江苏省高邮中学2009届高三第一学期期末数学试卷.files/image474.gif) 的交点个数为2个.即
的交点个数为2个.即/江苏省高邮中学2009届高三第一学期期末数学试卷.files/image180.gif) 与
与/江苏省高邮中学2009届高三第一学期期末数学试卷.files/image182.gif) 的交点个数为2个. …………………………………16分
的交点个数为2个. …………………………………16分
江苏省高邮中学2009届高三第一学期期末模拟考试
数学试卷
Ⅱ卷(加试题部分)参考答案
1.解: /江苏省高邮中学2009届高三第一学期期末数学试卷.files/image477.gif) ,……………………………………………………… 5分
,……………………………………………………… 5分
圆/江苏省高邮中学2009届高三第一学期期末数学试卷.files/image188.gif) 在
在/江苏省高邮中学2009届高三第一学期期末数学试卷.files/image186.gif) 的作用下的新曲线的方程为
的作用下的新曲线的方程为/江苏省高邮中学2009届高三第一学期期末数学试卷.files/image479.gif) ……10分
……10分
/江苏省高邮中学2009届高三第一学期期末数学试卷.files/image480.gif) 2.已知椭圆的长轴长为6,焦距
2.已知椭圆的长轴长为6,焦距/江苏省高邮中学2009届高三第一学期期末数学试卷.files/image190.gif) ,过椭圆左焦点F1作一直线,交椭圆于两点M、N,设
,过椭圆左焦点F1作一直线,交椭圆于两点M、N,设/江苏省高邮中学2009届高三第一学期期末数学试卷.files/image482.gif) ,当α为何值时,MN与椭圆短轴长相等?
,当α为何值时,MN与椭圆短轴长相等?
解:以椭圆的左焦点为极点长轴所在直线为
极轴建立极坐标系(如图)
这里:a=3,c=/江苏省高邮中学2009届高三第一学期期末数学试卷.files/image484.gif) ,
,
………………………2分
所以椭圆的极坐标方程为:
/江苏省高邮中学2009届高三第一学期期末数学试卷.files/image486.gif) ………………………4分
………………………4分
设M点的极坐标为/江苏省高邮中学2009届高三第一学期期末数学试卷.files/image488.gif) ,N点的极坐标为
,N点的极坐标为/江苏省高邮中学2009届高三第一学期期末数学试卷.files/image490.gif) ,………………5分
,………………5分
/江苏省高邮中学2009届高三第一学期期末数学试卷.files/image492.gif)
解法二:设椭圆的方程为/江苏省高邮中学2009届高三第一学期期末数学试卷.files/image494.gif) ,其左焦点为
,其左焦点为/江苏省高邮中学2009届高三第一学期期末数学试卷.files/image496.gif) ,直线MN的参数方程为:
,直线MN的参数方程为:
/江苏省高邮中学2009届高三第一学期期末数学试卷.files/image498.gif) ,
………………4分
,
………………4分
将此参数方程代人椭圆方程并整理得:
/江苏省高邮中学2009届高三第一学期期末数学试卷.files/image500.gif)
/江苏省高邮中学2009届高三第一学期期末数学试卷.files/image502.gif) ,设M、N对应的参数分别为
,设M、N对应的参数分别为/江苏省高邮中学2009届高三第一学期期末数学试卷.files/image504.gif) ,则
,则
2解:(1)以O为原点,OB,OC,OA分别为x,y,z轴建立空间直角坐标系.
则有A(0,0,1),B(2,0,0),C(0,2,0),E(0,1,0).
/江苏省高邮中学2009届高三第一学期期末数学试卷.files/image506.gif) ……………………2分
……………………2分
cos</江苏省高邮中学2009届高三第一学期期末数学试卷.files/image508.gif) >
>/江苏省高邮中学2009届高三第一学期期末数学试卷.files/image510.gif) .
………………………………4分
.
………………………………4分
由于异面直线BE与AC所成的角是锐角,故其余弦值是/江苏省高邮中学2009届高三第一学期期末数学试卷.files/image512.gif) .………………5分
.………………5分
/江苏省高邮中学2009届高三第一学期期末数学试卷.files/image514.jpg) (2)
(2)/江苏省高邮中学2009届高三第一学期期末数学试卷.files/image516.gif) ,
,/江苏省高邮中学2009届高三第一学期期末数学试卷.files/image518.gif) ,设平面ABE的法向量为
,设平面ABE的法向量为/江苏省高邮中学2009届高三第一学期期末数学试卷.files/image520.gif) ,
,
则由/江苏省高邮中学2009届高三第一学期期末数学试卷.files/image522.gif) ,
,/江苏省高邮中学2009届高三第一学期期末数学试卷.files/image524.gif) ,得
,得/江苏省高邮中学2009届高三第一学期期末数学试卷.files/image526.gif)
取n=(1,2,2),
平面BEC的一个法向量为n2=(0,0,1),
………………………………7分
/江苏省高邮中学2009届高三第一学期期末数学试卷.files/image528.gif) .
.
…………………………………9分
由于二面角A-BE-C的平面角是n1与n2的夹角的补角,其余弦值是-/江苏省高邮中学2009届高三第一学期期末数学试卷.files/image530.gif) .…… 10分
.…… 10分
4.解:(1)记"一次取出的3张卡片上的数字互不相同的事件"为A,
则/江苏省高邮中学2009届高三第一学期期末数学试卷.files/image532.gif) ………………………………………………2分
………………………………………………2分
(2)由题意/江苏省高邮中学2009届高三第一学期期末数学试卷.files/image195.gif) 有可能的取值为:2,3,4,5
有可能的取值为:2,3,4,5
/江苏省高邮中学2009届高三第一学期期末数学试卷.files/image534.gif)
/江苏省高邮中学2009届高三第一学期期末数学试卷.files/image536.gif)
/江苏省高邮中学2009届高三第一学期期末数学试卷.files/image538.gif)
/江苏省高邮中学2009届高三第一学期期末数学试卷.files/image540.gif)
/江苏省高邮中学2009届高三第一学期期末数学试卷.files/image542.gif)
/江苏省高邮中学2009届高三第一学期期末数学试卷.files/image544.gif)
/江苏省高邮中学2009届高三第一学期期末数学试卷.files/image546.gif)
/江苏省高邮中学2009届高三第一学期期末数学试卷.files/image548.gif) ………5分
………5分
所以随机变量/江苏省高邮中学2009届高三第一学期期末数学试卷.files/image195.gif) 的概率分布为:
的概率分布为:
/江苏省高邮中学2009届高三第一学期期末数学试卷.files/image195.gif)
2
3
4
5
P
/江苏省高邮中学2009届高三第一学期期末数学试卷.files/image550.gif)
/江苏省高邮中学2009届高三第一学期期末数学试卷.files/image552.gif)
/江苏省高邮中学2009届高三第一学期期末数学试卷.files/image554.gif)
/江苏省高邮中学2009届高三第一学期期末数学试卷.files/image556.gif)
所以/江苏省高邮中学2009届高三第一学期期末数学试卷.files/image195.gif) 的数学期望为E
的数学期望为E/江苏省高邮中学2009届高三第一学期期末数学试卷.files/image195.gif) =
=/江苏省高邮中学2009届高三第一学期期末数学试卷.files/image558.gif)
/江苏省高邮中学2009届高三第一学期期末数学试卷.files/image550.gif) +
+/江苏省高邮中学2009届高三第一学期期末数学试卷.files/image560.gif)
/江苏省高邮中学2009届高三第一学期期末数学试卷.files/image552.gif) +
+/江苏省高邮中学2009届高三第一学期期末数学试卷.files/image562.gif)
/江苏省高邮中学2009届高三第一学期期末数学试卷.files/image554.gif) +
+/江苏省高邮中学2009届高三第一学期期末数学试卷.files/image564.gif)
/江苏省高邮中学20 </div>
</div>
<div class=)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com