练习册

  • 练习册
  • 试题
    直线:．学科网 【查看更多】

     

    题目列表(包括答案和解析)

    椭圆G：的两个焦点为是椭圆上一点，且满．[来源:学#科#网]

    （１）求离心率的取值范围；

    （２）当离心率取得最小值时，点到椭圆上点的最远距离为．

    ①求此时椭圆G的方程；

    ②设斜率为的直线与椭圆G相交于不同两点，为的中点，问：

     

    查看答案和解析>>

    已知函数，给出下列四个命题：

    ①若

    ②的最小正周期是；

    ③在区间上是增函数；[来源:学科网]

    ④的图象关于直线对称；

    ⑤当时，的值域为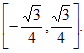

    其中正确的命题为                            （    ）

           A．①②④     B．③④⑤     C．②③       D．③④

    查看答案和解析>>

    给出下列四个命题：

        ①若集合A，B满足，则；

        ②给定命题，若“”为真，则“”为真；

        ③设若，则；[来源:学科网]

        ④若直线与直线垂直，则.

    其中正确命题的个数是            （    ）

        A．1    B．2    C．3    D．4

    查看答案和解析>>

    如图为双曲线的两焦点，以为直径的圆与双曲线交于是圆与轴的交点，连接与交于，且是的中点，学科网

    （1）当时，求双曲线的方程；学科网                                                                                                                                                                    

    （2）试证：对任意的正实数，双曲线的离心率为常数．

    查看答案和解析>>

    已知函数，给出下列四个命题：学科网

         ①若，则；   ②的最小正周期是；学科网

         ③在区间上是增函数；  ④的图象关于直线对称学科网

         A．①②④     B．①③     C．②③     D．③④学科网

    查看答案和解析>>

    或或7                   ………………………………14分

    16．（本小题满分14分）

    (1)证明：E、P分别为AC、A′C的中点，

            EP∥A′A，又A′A平面AA′B，EP平面AA′B

           ∴即EP∥平面A′FB                  …………………………………………5分

    (2) 证明：∵BC⊥AC，EF⊥A′E，EF∥BC

       ∴BC⊥A′E，∴BC⊥平面A′EC

         BC平面A′BC

       ∴平面A′BC⊥平面A′EC             …………………………………………9分

    (3)证明：在△A′EC中，P为A′C的中点，∴EP⊥A′C，

      在△A′AC中，EP∥A′A，∴A′A⊥A′C

          由(2)知：BC⊥平面A′EC   又A′A平面A′EC

          ∴BC⊥AA′

          ∴A′A⊥平面A′BC                   …………………………………………14分

    ∴                    …………………………………………15分

    （本题也可以利用特征三角形中的有关数据直接求得）

    18．（本小题满分15分）

    （1）延长BD、CE交于A，则AD=，AE=2

         则S△ADE= S△BDE= S△BCE=

          ∵S△APQ=，∴

          ∴             …………………………………………7分

    （2）

              =?

    …………………………………………12分

        当，

    即，            

    …………………………………………15分

    （3）

    设上式为 ，假设取正实数，则?

    当时，，递减；

    当，，递增． ……………………………………12分

                    

        

    ∴不存在正整数，使得

    即                  …………………………………………16分

    ，显然成立             ……………………………………12分

    当时，，

    使不等式成立的自然数n恰有4个的正整数p值为3

                              ……………………………………………16分

     

     

     

     

     

     

     

    泰州市2008～2009学年度第二学期期初联考

    高三数学试题参考答案

    附加题部分

    度单位．（1），，由得．

    所以．

    即为圆的直角坐标方程．  ……………………………………3分

    同理为圆的直角坐标方程． ……………………………………6分

    （2）由　　　　　　

    相减得过交点的直线的直角坐标方程为． …………………………10分

    D．证明：（1）因为

        所以          …………………………………………4分

        （2）∵   …………………………………………6分

        同理，，……………………………………8分

        三式相加即得……………………………10分

    22．（必做题）（本小题满分10分）

    解：（1）记“恰好选到1个曾经参加过数学研究性学习活动的同学”为事件的, 则其概率为                …………………………………………4分

        答：恰好选到1个曾经参加过数学研究性学习活动的同学的概率为

    （1），，，

    ，

                  ……………………………………3分

    （2）平面BDD1的一个法向量为

    设平面BFC1的法向量为

    ∴

    取得平面BFC1的一个法向量

    ∴所求的余弦值为                     ……………………………………6分

    （3）设（）

    ，由得

    即，

    当时，

    当时，∴   ……………………………………10分

     


    同步练习册答案