
题目列表(包括答案和解析)
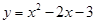 与x轴交于点A和点B,与y轴相交于点C.
与x轴交于点A和点B,与y轴相交于点C.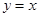 上的一个动点,点Q是抛物线上的一个动点,若以点O,C,P和Q为顶点的四边形为直角梯形,求相应的点P的坐标.
上的一个动点,点Q是抛物线上的一个动点,若以点O,C,P和Q为顶点的四边形为直角梯形,求相应的点P的坐标.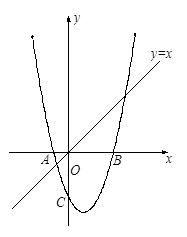
如图1,已知抛物线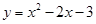 与x轴交于点A和点B,与y轴相交于点C.
与x轴交于点A和点B,与y轴相交于点C.
【小题1】求A、B、C三点的坐标
【小题2】点D为射线CB上的一动点(点D、B不重合),过点B作x轴的垂线BE与以点D为顶点的抛物线y=(x-t)2+h相交于点E,从△ADE和△ADB中任选一个三角形,求出当其面积等于△ABE的面积时的t的值;(友情提示:1、只选取一个三角形求解即可;2、若对两个三角形都作了解答,只按第一个解答给分.)
【小题3】如图2,若点P是直线 上的一个动点,点Q是抛物线上的一个动点,若以点O,C,P和Q为顶点的四边形为直角梯形,求相应的点P的坐标.
上的一个动点,点Q是抛物线上的一个动点,若以点O,C,P和Q为顶点的四边形为直角梯形,求相应的点P的坐标.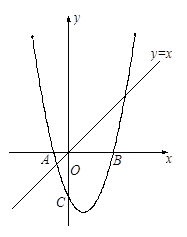


 暗反应中 45.下表为某同学探究影响植物光合作用因素所做的实验。据图表可知,探究的影响因素有 。要比较不同颜色的光对光合作用的影响,应选择的容器标
暗反应中 45.下表为某同学探究影响植物光合作用因素所做的实验。据图表可知,探究的影响因素有 。要比较不同颜色的光对光合作用的影响,应选择的容器标 号是 。
号是 。| 容器 | 植物 | 部位 | 光质 | 温度(℃) | O2增加量(mL/8小时) |
| 1 | 天竺葵 | 叶 | 红 | 22 | 120 |
| 2 | 天竺 葵 葵 | 叶 | 黄 | 22 | 15 |
| 3 | 天竺葵 | 根 | 红 | 22 | -10 |
| 4 | 紫罗兰 | 叶 | 红 | 22 | 80 |
| 5 | 紫罗兰 | 叶 | 黄 | 22 | 10 |

二次函数y=﹣x2+2x+m的图象与x轴交于A.B两点(B在A右侧),顶点为C,且A.B两点间的距离等于点C到x轴的距离的2倍.
(1)求此抛物线的解析式.
(2)求直线BC的解析式.
(3)若点P在抛物线的对称轴上,且⊙P与x轴以及直线BC都相切,求点P的坐标.
【提示:( +1)(
+1)( -1)=1】
-1)=1】
二次函数y=﹣x2+2x+m的图象与x轴交于A.B两点(B在A右侧),顶点为C,且A.B两点间的距离等于点C到x轴的距离的2倍.
(1)求此抛物线的解析式.
(2)求直线BC的解析式.
(3)若点P在抛物线的对称轴上,且⊙P与x轴以及直线BC都相切,求点P的坐标.
【提示:( +1)(
+1)( -1)=1】
-1)=1】
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com